
分析 (1)将所有行驶记录相加,再根据正负数的意义判断;
(2)求出所有行驶记录绝对值的和,然后乘以0.0642计算即可得解.
解答 解:(1)18.3-9.5+7.1-14-6.2+13-6.8-8.5,
=18.3+7.1+13-9.5-14-6.2-6.8-8.5,
=38.4-45,
=-6.6(千米),
所以,B地在A地南方,相距6.6千米;
(2)18.3+9.5+7.1+14+6.2+13+6.8+8.5=83.5(千米),
83.5×0.0642=5.3607≈5.4(升).
点评 此题主要考查了正负数的意义,解题关键是理解“正”和“负”的相对性,明确什么是一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.


科目:初中数学 来源: 题型:解答题
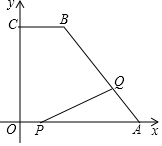 如图,在平面直角坐标系中,已知点A(10,0),B(4,8)C(0,8),连接AB,BC,点P从坐标原点O出发,以每秒1个单位长度的速度向点A运动,同时,点Q从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,当其中一点到达终点时,另一点也随之停止运动,设两点运动的时间为t秒,请解答下列问题:
如图,在平面直角坐标系中,已知点A(10,0),B(4,8)C(0,8),连接AB,BC,点P从坐标原点O出发,以每秒1个单位长度的速度向点A运动,同时,点Q从点A出发,以每秒2个单位长度的速度沿折线A-B-C向点C运动,当其中一点到达终点时,另一点也随之停止运动,设两点运动的时间为t秒,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
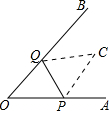 已知∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2,将∠O沿PQ折叠,点O落在平面内的点C处
已知∠AOB=45°,点P、Q分别是边OA、OB上的两点,且OP=2,将∠O沿PQ折叠,点O落在平面内的点C处查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
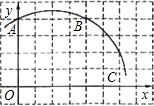 如图,已知直角坐标系中,A(0,4)、B(4,4)、C(6,2),
如图,已知直角坐标系中,A(0,4)、B(4,4)、C(6,2),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com