
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④方程ax2+bc+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
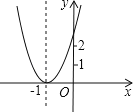
A.2 B.3 C.4 D.5
【答案】C
【解析】
试题分析:①首先根据抛物线开口向上,可得a>0;然后根据对称轴在y轴左边,可得b>0;最后根据抛物线与y轴的交点在x轴的上方,可得c>0,据此判断出abc>0即可.
②根据二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,可得△=0,即b2﹣4a(c+2)=0,b2﹣4ac=8a>0,据此解答即可.
③首先根据对称轴x=﹣![]() =﹣1,可得b=2a,然后根据b2﹣4ac=8a,确定出a的取值范围即可.
=﹣1,可得b=2a,然后根据b2﹣4ac=8a,确定出a的取值范围即可.
④根据顶点为(﹣1,0),可得方程ax2+bc+c=﹣2的有两个相等实根,
⑤根据点BC在对称轴右侧,y随x的增大而增大来判断即可.
解:∵抛物线开口向上,
∴a>0,
∵对称轴在y轴左边,
∴b>0,
∵抛物线与y轴的交点在x轴的上方,
∴c+2>2,
∴c>0,
∴abc>0,
∴结论①正确;
∵二次函数y=ax2+bx+c+2的图象与x轴只有一个交点,
∴△=0,
即b2﹣4a(c+2)=0,
∴b2﹣4ac=8a>0,
∴结论②不正确;
∵对称轴x=﹣![]() =﹣1,
=﹣1,
∴b=2a,
∵b2﹣4ac=8a,
∴4a2﹣4ac=8a,
∴a=c+2,
∵c>0,
∴a>2,
∴结论③正确;
∵二次函数y=ax2+bx+c+2的顶点为(﹣1,0),
∴方程ax2+bx+c+2=0的根为x1=x2=﹣1;
∴结论④正确;
∵x>﹣1,y随x的增大而增大,
∴y1>y2,
∴结论⑤正确.
综上,可得正确结论的个数是2个:①③④⑤.
故选C.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】观察下列等式:
阅读下列材料:
1×2=![]() (1×2×3﹣0×1×2),
(1×2×3﹣0×1×2),
2×3=![]() (2×3×4﹣1×2×3),
(2×3×4﹣1×2×3),
3×4=![]() (3×4×5﹣2×3×4),
(3×4×5﹣2×3×4),
由以上三个等式相加,可得1×2+2×3+3×4=![]() ×3×4×5=20
×3×4×5=20
读完以上材料,请你计算下列各题,其中(1)需要写出过程,其它试题直接写出答案.
(1)1×2+2×3+3×4+…+6×7= ;
(2)1×2+2×3+3×4+…+n×(n+1)= ;
(3)1×2+2×3+3×4+3×4×5+…+6×7×8= ;
(4)1×2+2×3+3×4+3×4×5+…+n×(n+1)×(n+2)= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+1的图象与y轴交于点A,与反比例函数y=![]() 在第一象限内的图象交于点B,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=
在第一象限内的图象交于点B,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
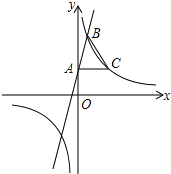
(1)求反比例函数的表达式及△ABC的面积;
(2)直接写出当x<1时,y=![]() (k≠0)中y的取值范围.
(k≠0)中y的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形OABC是矩形,ADEF是正方形,点A,D在x轴的正半轴,点C在y轴的正半轴上,点F再AB上,点B,E在反比例函数y=![]() 的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
的图象上,OA=2,OC=6,则正方形ADEF的边长为 .
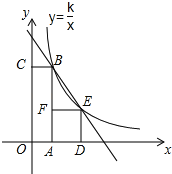
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列等式错误的是( )
A. (2mn)2=4m2n2 B. (﹣2mn)2=4m2n2
C. (2m2n2)3=8m6n6 D. (﹣2m2n2)3=﹣8m5n5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC为等边三角形,D、E分别是AC、BC上的点,且AD=CE,AE与BD相交于点P,
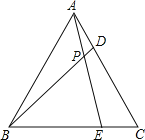
(1)求∠BPE的度数;
(2)若BF⊥AE于点F,试判断BP与PF的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】分别有下列几组数据:①6、8、10 ②12、13、5 ③ 17、8 、15 ④4、11、9其中能构成直角三形的有( )
A. 4组 B. 3组 C. 2组 D. 1组
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com