
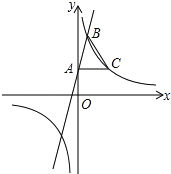
【题目】如图,在平面直角坐标系xOy中,一次函数y=3x+1的图象与y轴交于点A,与反比例函数y=![]() 在第一象限内的图象交于点B,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=
在第一象限内的图象交于点B,且点B的横坐标为1,过点A作AC⊥y轴交反比例函数y=![]() (k≠0)的图象于点C,连接BC.
(k≠0)的图象于点C,连接BC.
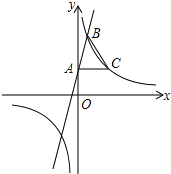
(1)求反比例函数的表达式及△ABC的面积;
(2)直接写出当x<1时,y=![]() (k≠0)中y的取值范围.
(k≠0)中y的取值范围.
【答案】(1)y=![]() ,S△ABC=
,S△ABC=![]() ACBD=
ACBD=![]() ×4×3=6;(2)当x<0时,y<0.
×4×3=6;(2)当x<0时,y<0.
【解析】
试题分析:(1)先由一次函数y=3x+1的图象过点B,且点B的横坐标为1,将x=1代入y=3x+1,求出y的值,得到点B的坐标,再将B点坐标代入y=![]() ,利用待定系数法即可求出反比例函数的表达式;根据一次函数y=3x+1的图象与y轴交于点A,求出点A的坐标为(0,1),再将y=1代入y=
,利用待定系数法即可求出反比例函数的表达式;根据一次函数y=3x+1的图象与y轴交于点A,求出点A的坐标为(0,1),再将y=1代入y=![]() ,求出x的值,那么AC=4.过B作BD⊥AC于D,则BD=yB﹣yC=4﹣1=3,然后根据S△ABC=
,求出x的值,那么AC=4.过B作BD⊥AC于D,则BD=yB﹣yC=4﹣1=3,然后根据S△ABC=![]() ACBD,将数值代入计算即可求解;
ACBD,将数值代入计算即可求解;
(2)根据x<1时,得到![]() ,于是得到y的取值范围.
,于是得到y的取值范围.
解:(1)∵一次函数y=3x+1的图象过点B,且点B的横坐标为1,
∴y=3×1+1=4,
∴点B的坐标为(1,4).
∵点B在反比例函数y=![]() 的图象上,
的图象上,
∴k=1×4=4,
∴反比例函数的表达式为y=![]() ,
,
∵一次函数y=3x+1的图象与y轴交于点A,
∴当x=0时,y=1,
∴点A的坐标为(0,1),
∵AC⊥y轴,
∴点C的纵坐标与点A的纵坐标相同,是1,
∵点C在反比例函数y=![]() 的图象上,
的图象上,
∴当y=1时,1=![]() ,解得x=4,
,解得x=4,
∴AC=4.
过B作BD⊥AC于D,则BD=yB﹣yC=4﹣1=3,
∴S△ABC=![]() ACBD=
ACBD=![]() ×4×3=6;
×4×3=6;
(2)由图形得:∵当0<x<1时,![]() ,
,
∴y>4,
当x<0时,y<0.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A. 面积相等的两个三角形全等 B. 周长相等的两个三角形全等
C. 形状相同的两个三角形全等 D. 成轴对称的两个三角形全等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在平面直角坐标系中,抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,顶点为A.
,顶点为A.
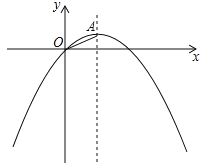
(1)求抛物线的表达式及顶点A的坐标;
(2)点P为抛物线对称轴上一点,联结OA、OP.
①当OA⊥OP时,求OP的长;
②过点P作OP的垂线交对称轴右侧的抛物线于点B,联结OB,当∠OAP=∠OBP时,求点B的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】方程x(4x+3)=3x+1化为一般形式 ____________,它的二次项系数是______,
一次项系数是_________,常数项是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】直角坐标系中,点P(x,y)在第二象限,且P 到x 轴、y 轴距离分别为3,7,则P 点坐标为( )
A. (-3,7) B. (-7,3) C. (3,7) D. (7,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c+2的图象如图所示,顶点为(﹣1,0),下列结论:①abc>0;②b2﹣4ac=0;③a>2;④方程ax2+bc+c=﹣2的根为x1=x2=﹣1;⑤若点B(﹣![]() ,y1),C(﹣
,y1),C(﹣![]() ,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
,y2)为函数图象上的两点,则y2<y1,其中正确的个数是( )
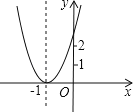
A.2 B.3 C.4 D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】神农尝百草,泡泡青菜便是其中之一,小随同学利用假期开网店批发出售泡泡青菜,他打出促销广告:最优质泡泡青菜35箱,每箱售价30元,若一次性购买不超过10箱时,售价不变;若一次性购买超过10箱时,没多买1箱,所买的每箱泡泡青菜的售价均降低0.3元.已知该青菜成本是每箱20元,若不计其他费用,设顾客一次性购买泡泡青菜x(x为整数)箱时,该网店从中获利y元.
(1)求y与x的函数关系式,并写出自变量x的取值范围;
(2)顾客一次性购买多少箱时,该网店从中获利最多,最多是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列条件中能得到平行线的是( )
①邻补角的角平分线;②平行线内错角的角平分线;③平行线同旁内角的角平分线.
A. ①② B. ②③ C. ② D. ③
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com