
����Ŀ�������ķ��ദ����������ã����Լ�����Ⱦ����ʡ��Դ��ij���л�������Ϊ���������ʵЧ�����������˲��־���С��һ��ʱ�������������ķ���������������Ϣ���£� 
����ͼ������������⣺
��1���뽫����ͳ��ͼ����������
��2���ڳ��������У��������к��������֣�
��3�����鷢�֣��ڿɻ�����������������ռ ![]() ��ÿ����1�������������ɻ��0.7�ֶ���ԭ�ϣ�����ó���ÿ�²�������������Ϊ5 000�֣���ȫ�����ദ������ôÿ�»��յ��������������Ի�ö��ٶֶ���ԭ�ϣ�
��ÿ����1�������������ɻ��0.7�ֶ���ԭ�ϣ�����ó���ÿ�²�������������Ϊ5 000�֣���ȫ�����ദ������ôÿ�»��յ��������������Ի�ö��ٶֶ���ԭ�ϣ�
���𰸡�
��1���⣺�۲�ͳ��ͼ֪��D��������5�֣�ռ10%��
����������Ϊ5��10%=50�֣�
��B����������50��30%=15�֣�
��ͳ�Ʊ�Ϊ��
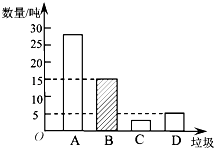
��2��3
��3���⣺ ![]() ���֣���
���֣���
��ÿ�»��յ��������������Ի��378�ֶ���ԭ��
���������⣺��2����C����ռ�İٷֱ�Ϊ��1��10%��30%��54%=6%�� ���к�����Ϊ��50��6%=3�֣�
��1������D������������ռ�İٷֱȼ����������������Ȼ���������ռ�İٷֱȼ������ÿ��С���Ƶ���Ӷ���ȫͳ��ͼ����2�����C����ռ�İٷֱȣ��������C���������������3��������ÿɻ�����������Ȼ��������Ͽ����ϼ��ɣ�


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ϸ�Ķ��������⣬������⣺
���⣺��֪��������ʽx2��4x��m��һ����ʽ�ǣ�x��3��������һ����ʽ�Լ�m��ֵ��
�⣺����һ����ʽΪ��x��n������ x2��4x��m����x��3����x��n��
�� x2��4x��m��x2����n��3��x��3n
��ã�n����7�� m����21 �� ��һ����ʽΪ��x��7����m��ֵΪ��21
���⣺�������Ϸ�������������⣺
��֪��������ʽ2x2��3x��k��һ����ʽ�ǣ�2x��5��������һ����ʽ�Լ�k��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���һ�ν���OAB�任����OA1B1���ڶ��ν���OA1B1�任����OA2B2�������ν�OA2B2�任����OA3B3����֪�任�����и�������ֱ�ΪA��1��3����A1��2��3����A2��4��3����A3��8��3����B��2��0����B1��4��0����B2��8��0����B3��16��0����
��1���۲�ÿ�α任ǰ����������кα仯���ҳ����ɣ����˹����ٽ���OA3B3�任����OA4B4����A4������Ϊ�� ����B4������Ϊ�� ����
��2�������Ϲ��ɽ���OAB����n�α任�õ���OAnBn����An������Ϊ�� ����Bn������Ϊ�� ����
��3����OAnBn������� ����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD�ǡ�O���ڽ��ı��Σ�AD���ӳ�����BC���ӳ����ཻ�ڵ�E��DC=DE�� 
��1����֤����A=��AEB��
��2�����DC��OE����֤����ABE�ǵȱ������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ֽƬABCD����ֱ������ϵ�У���A��4��0������B��0��3������D�����ڵ�B��C��Ϊ��BC�϶��㣬����O��D�۵�ֽƬ���õ�B����ۺ�OD������D�ٴ��۵�ֽƬ��ʹ��C����ֱ��DB���ϣ��õ�C����ۺ�DE������OE����BD=t��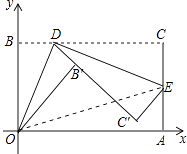
��1����t=1ʱ�����E�����ꣻ
��2����S�ı���OECB=s���ú�t��ʽ�ӱ�ʾs��Ҫ��д��t��ȡֵ��Χ����
��3����OEȡ��Сֵʱ�����E�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪�ڡ�ABC�У�AB=AC����BAC=90�㣬�ֱ��B��C���A��ֱ�������ߣ�����ֱ�ΪE��F��
��1����֤����ABE�ա�CAF
��2����ͼ�ٹ�A��ֱ����б��BC���ཻʱ����̽��EF�� BE��CF�����߶εĹ�ϵ��
��3����ͼ�ڹ�A��ֱ����б��BC�ཻʱ�������������䣬��BE=10��CF=3����FE����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��Rt��ABC�У���C=90�㣬AC=6��BC=8��ADƽ�֡�BAC�����B��AD�ľ����ǣ� �� 
A.3
B.4
C.2 ![]()
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ƽ��ֱ������ϵ�У�OΪ����ABCD�ĶԳ����ģ���֪C��2��0����D��0����1����NΪ�߶�CD��һ�㣨����C��D�غϣ���
��1������CΪ���㣬�Ҿ�����D�������߽���ʽ��
��2����N����BD�ĶԳƵ�ΪN1 �� N����BC�ĶԳƵ�ΪN2 �� ��֤����N1BN2�ס�ABC��
��3����2����N1N2����Сֵ��
��4������N��y���ƽ���߽���1���е��������ڵ�P����QΪֱ��AB�ϵ�һ�����㣬�ҡ�PQA=��BAC����PQ��Сʱ��Q���꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=2x+3��x�ύ�ڵ�A����y�ύ�ڵ�B��D������AB�ϵĶ��㣨�����A�غϣ���DN��x����N���ѡ�AND��ֱ��AB���ۣ��õ���AMD���ӳ�MA��y���ڵ�C����A��C��D�����ԲE��x�ύ�ڵ�F������DF�� 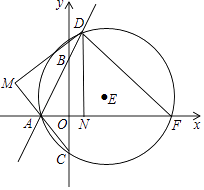
��1��ֱ��д��tan��BAO��ֵΪ��
��2����֤��MC=NF��
��3�����߶�OC�ij���
��4���Ƿ���ڵ�D��ʹDF��AC�������ڣ����D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com