如图.在梯形ABCD中.AD∥BC.点E在AB上.DE.CE分别是∠ADC和∠BCD的平分线.求∠DEC的度数．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

5．

如图，在梯形ABCD中，AD∥BC，点E在AB上，DE，CE分别是∠ADC和∠BCD的平分线，求∠DEC的度数．

分析由AD∥BC，推出∠ADC+∠BCD=180°，由DE，CE分别是∠ADC和∠BCD的平分线，推出2∠EDC+2∠ECD=180°，可得∠EDC+∠ECD=90°，由此即可解决问题．

解答解：∵AD∥BC，
∴∠ADC+∠BCD=180°，
∵DE，CE分别是∠ADC和∠BCD的平分线，
∴2∠EDC+2∠ECD=180°，
∴∠EDC+∠ECD=90°，
∴∠DEC=180°-90°=90°．

点评本题考查梯形的性质、平行线的性质、角平分线的定义等知识，解题的关键是灵活运用所学知识解决问题，属于中考基础题．

练习册系列答案

Happy寒假作业快乐寒假系列答案

金象教育U计划学期系统复习寒假作业系列答案

八斗才火线计划寒假西安交通大学出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：解答题

15．

为了解某校七年级学生的身高情况，随机抽取该校男生、女生进行抽样调查，已知抽取的样本中，男生、女生的人数相同，利用所得数据绘制如下统计图表：
身高情况分组表（单位：cm）

组别	身高
A	145≤x＜155
B	155≤x＜160
C	160≤x＜165
D	165≤x＜170
E	170≤x＜175

根据图表提供的信息，回答下列问题：
（1）样本中，男生人数为40人，男生身高类别C的组中值为162.5，男生身高类别B的频率为0.3；
（2）样本中，女生身高在E组的人数为2人，女生类别D的频数所对应的扇形圆心角为54°；
（3）已知该校共有男生400人，女生380人，请估计身高在160≤x＜170之间的学生约有多少人？

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

16．

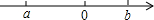实数a、b在数轴上的位置如图，化简：$\sqrt{{a}^{2}}-\sqrt{{b}^{2}}-\sqrt{（a-b）^{2}}$
思路分析：因为a-b是一个负数，所以$\sqrt{（a-b）^{2}}=b-a$
规范解答：由a、b所在数轴上的位置可以得到a＜0，b＞0．
a-b＜0，
$\sqrt{{a}^{2}}$=|a|=-a，
$\sqrt{{b}^{2}}$=|b|=b，
$\sqrt{（a-b）^{2}}$=|a-b|=-a+b．所以原式=-a-b-（-a+b）=-2b．

查看答案和解析>>

科目：初中数学 来源： 题型：解答题

13．