
 有一个点到达点C时,另一点也停止移动,若移动的时间为t秒,△DPQ的面积为S个平方单位.
有一个点到达点C时,另一点也停止移动,若移动的时间为t秒,△DPQ的面积为S个平方单位. t2(0<t≤1),S=
t2(0<t≤1),S= t(1<t≤2),S=-
t(1<t≤2),S=- t2+
t2+ t(2<<3).
t(2<<3). t=
t= ,
, .
. .
. ,有3种情况:①0<t≤1时,根据三角形的面积公式求出即可;②1<t≤2时,根据三角形的面积公式求出即可;③当2<t<3时,根据三角形的面积求出即可;
,有3种情况:①0<t≤1时,根据三角形的面积公式求出即可;②1<t≤2时,根据三角形的面积公式求出即可;③当2<t<3时,根据三角形的面积求出即可;

 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:
 如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.
如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.查看答案和解析>>
科目:初中数学 来源: 题型:
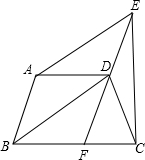 如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.
如图所示,等腰梯形ABCD中,AD∥BC,DF∥AB交BC于F点,AE∥BD交FD的延长线于E点.| 1 | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.
20、现有5张如图所示的等腰梯形纸片,打算用其中的若干张来拼成较大的等腰梯形,你能拼出哪几种不同的等腰梯形?分别画出它们的示意图,并写出它们的周长.查看答案和解析>>
科目:初中数学 来源: 题型:
 如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD
如图所示,等腰梯形ABCD中,AD∥BC,AB=DC,AC⊥BD,延长BC至点E,使得CE=AD查看答案和解析>>
科目:初中数学 来源: 题型:
 已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,
已知:如图所示,等腰梯形ABCD中,AB∥CD,AD=BC=4,DC=3,△ADE≌△ECB,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com