
【题目】新规定:点![]() 为线段
为线段![]() 上一点,当
上一点,当![]() 或
或![]() 时,我们就规定
时,我们就规定![]() 为线段
为线段![]() 的“三倍距点”。如图,在数轴上,点
的“三倍距点”。如图,在数轴上,点![]() 所表示的数为-3,点
所表示的数为-3,点![]() 所表示的数为5.
所表示的数为5.

(1)确定点![]() 所表示的数为___________.
所表示的数为___________.
(2)若动点![]() 从点
从点![]() 出发,沿射线
出发,沿射线![]() 方向以每秒2个单位长度的速度运动,设运动时间为
方向以每秒2个单位长度的速度运动,设运动时间为![]() 秒.
秒.
①当点![]() 与点
与点![]() 重合时,求
重合时,求![]() 的值.
的值.
②求![]() 的长度(用含
的长度(用含![]() 的代数式表示).
的代数式表示).
③当点![]() 为线段
为线段![]() 的“三倍距点”时,直接写出
的“三倍距点”时,直接写出![]() 的值.
的值.
【答案】(1)1或3;(2)①4;②当点P在点A右侧时,![]() ;当点P在点A左侧时,
;当点P在点A左侧时,![]() ;③16或
;③16或![]() .
.
【解析】
(1)设点C所表示的数为c,根据定义即可求出答案;
(2)①根据路程、时间、速度之间的关系即可求出答案;
②根据点P的位置即可求出AP的表达式;
③根据“三倍距点”的定义列出方程求出答案即可.
解:(1)设点C所表示的数为c,
当CA=3CB时,
c+3=3(5c),
解得:c=3,
当CB=3CA时,
5c=3(c+3),
解得:c=1
故答案为:1或3.
(2)①∵![]() ,
,
∴t=8÷2=4,
答:当点P与点A重合时,t的值为4.
②当点P在点A右侧时,![]() ;
;
当点P在点A左侧时,![]() .
.
③设点P所表示的数为p,
当PA=3AB时,
此时3p=3×8,
解得:p=27,
∴BP=5+27=32,
∴![]() ,
,
当AB=3PA时,
∴8=3(3p),
解得:![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴综上所述,t=16或![]() .
.


 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
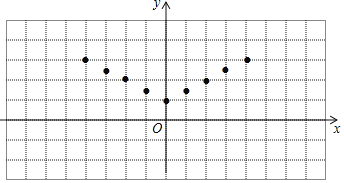
【题目】某校数学兴趣小组根据学习函数的经验,对函数y=![]() |x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
|x|+1的图象和性质进行了探究,探究过程如下:(1)自变量x的取值范围是全体实数,x与y的几组对应值如表:
X | … | ﹣4 | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
Y | … | 3 | 2.5 | m | 1.5 | 1 | 1.5 | 2 | 2.5 | 3 | … |
(1)其中m= .
(2)如图,在平面直角坐标系xOy中,描出了上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(3)当2<y≤3时,x的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:①已知A(x1,y1)、B(x2,y2),则AB=![]() ;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离
;② 已知A(x0,y0)直线 l 的方程为 Ax By C 0, 则 A 到直线的距离![]()
(1)已知 A2,5、 B1,1,求 AB ;
(2)已知 A2,1,直线l : 3x 4y 5 0,求 A 到直线的距离;
(3)求两平行直线3x 4y1 0与3x 4 y 8 0之间的距离;
(4)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
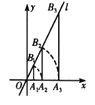
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作不轴的垂线交直
作不轴的垂线交直![]() 于点
于点![]() 以原点
以原点![]() 为圆心,
为圆心,![]() 的长为半径断弧交
的长为半径断弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此作法进行下去,则
;…按此作法进行下去,则![]() 的长是____________.
的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
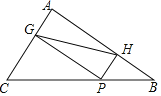
【题目】如图,在△ABC中,AC=9,AB=12,BC=15,P为BC边上一动点,PG⊥AC于点G,PH⊥AB于点H.
(1)求证:四边形AGPH是矩形;
(2)在点P的运动过程中,GH的长度是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
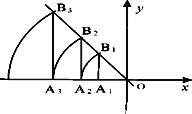
【题目】如图,直线l:y=-![]() x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
x,点A1坐标为(-4,0).过点A1作x轴的垂线交直线l于点B1,以原点O为圆心,OB1长为半径画弧交x轴负半轴于点A2,再过点A2作x轴的垂线交直线l于点B2,以原点O为圆心,OB2长为半径画弧交x轴负半轴于点A3,…,按此做法进行下去,点A2018的坐标为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com