[题目]计算:(1)(-1)-(-3) (2) (3)[(-56)×()+] (4) 题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】计算：

(1)（-1）-（-3）

(2)

(3)[（-56）×（）+]

(4)

【答案】(1)2;(2)31;(3)-9;(4)

【解析】

（1）由题意先去括号，再利用有理数加减法法则进行计算即可求出值；

（2）根据题意先计算乘除法运算，再计算加法运算即可求出值；

（3）根据题意先计算乘方运算，再运用乘法分配律计算乘法运算，最后算加减运算即可求出值；

（4）由题意利用度分秒运算的方法先进行乘除运算，最后算减法运算即可求出值．

解：（1）（-1）-（-3）

=-1+3

=2；

(2)

=-1+32

=31；

(3)[（-56）×（）+]

=-8-（-32+21-4+16）

=-8-1

=-9；

(4)

=33°4′-11°30′

=21°34'．

练习册系列答案

衡水示范高中假期伴学出彩方案光明日报出版社系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

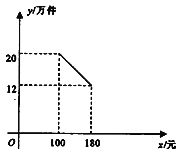
【题目】杰瑞公司成立之初投资1500万元购买新生产线生产新产品，此外，生产每件该产品还需要成本60元.按规定，该产品售价不得低于100元/件且不得超过180元/件，该产品销售量y（万件）与产品售价x（元）之间的函数关系如图所示.

(1)求y与x之间的函数关系式，并写出x的取值范围；

(2)第一年公司是盈利还是亏损？求出当盈利最大或者亏损最小时的产品售价；

(3)在(2)的前提下，即在第一年盈利最大或者亏损最小时，第二年公司重新确定产品售价，能否使两年共盈利达1340万元，若能，求出第二年产品售价；若不能，请说明理由.

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图：数轴上有、两点，分别对应的数为，，已知与互为相反数，点为数轴上一动点，对应为．

(1)若点到点和点的距离相等，求点对应的数；

(2)数轴上是否存在点，使点到点和点的距离之和为5?若存在，请求出的值，若不存在，请说明理由；

(3)当点以每分钟1个单位长度的速度从点向左运动，点以每分钟5个单位长度向左运动，点以每分钟20个单位长度的速度向左运动，问几分钟时点到点、点的距离相等．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，四边形OP1A1B1、A1P2A2B2、A2P3A3B3、……、An－1PnAnBn都是正方形，对角线OA1、A1A2、A2A3、……、An－1An都在y轴上(n≥2)，点P1(x1，y1)，点P2(x2，y2)，……，点Pn(xn，yn)在反比例函数y＝ (x＞0)的图象上，已知B1 (－1，1)。