
【题目】已知,点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,
,![]() 为原点,且
为原点,且![]() 、
、![]() 满足:
满足:![]() .试解答下列问题:
.试解答下列问题:
(1)求数轴上线段![]() 的长度;
的长度;
(2)若点![]() 以每秒2个单位长度的速度沿数轴向右运动,则经过
以每秒2个单位长度的速度沿数轴向右运动,则经过![]() 秒后点
秒后点![]() 表示的数为 ;(用含
表示的数为 ;(用含![]() 的代数式表示)
的代数式表示)
(3)若点![]() ,
,![]() 都以每秒2个单位长度的速度沿数轴向右运动,而点
都以每秒2个单位长度的速度沿数轴向右运动,而点![]() 不动,经过
不动,经过![]() 秒后其中一个点是一条线段的中点,求此时
秒后其中一个点是一条线段的中点,求此时![]() 的值.
的值.
![]()
【答案】(1)6;(2)![]() ;(3)当
;(3)当![]() 值为
值为![]() 时点
时点![]() 为线段
为线段![]() 的中点,当
的中点,当![]() 值为5时点
值为5时点![]() 为线段
为线段![]() 的中点.
的中点.
【解析】
(1)根据绝对值及偶次方的非负性,即可得出a、b的值,进而即可求出线段AB的长度;
(2)根据-4+点A运动的速度×t=经过t秒后点A表示的数,即可得出结论;
(3)找出t秒后点A、B表示的数,分点O为线段AB的中点及点A为线段OB的中点两种情况考虑:①当点O为线段AB的中点时,根据中点坐标公式即可求出此时的t值;②当点A为线段OB的中点时,根据中点坐标公式即可求出此时的t值.综上即可得出结论.
(1)![]() ,
,
![]() ,
,![]() ,
,
![]() .
.
(2)![]() 秒后点
秒后点![]() 表示的数为
表示的数为![]() .
.
故答案为:![]() .
.
(3)![]() 秒后点
秒后点![]() 表示的数为
表示的数为![]() ,点
,点![]() 表示的数为
表示的数为![]() .
.
①当点![]() 为线段
为线段![]() 的中点时,有
的中点时,有![]() ,
,
解得:![]() ;
;
②当点![]() 为线段
为线段![]() 的中点时,有
的中点时,有![]() ,
,
解得:![]() .
.
综上所述:当![]() 值为
值为![]() 时点
时点![]() 为线段
为线段![]() 的中点,当
的中点,当![]() 值为5时点
值为5时点![]() 为线段
为线段![]() 的中点.
的中点.


科目:初中数学 来源: 题型:
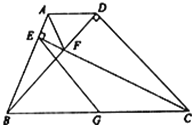
【题目】如图,四边形ABCD中,AD∥BC,∠DCB=45°,CD=2,BD⊥CD.过点C作CE⊥AB于E,交对角线BD于F,点G为BC中点,连接EG、AF.
(1)求EG的长;
(2)求证:CF=AB+AF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AD平分∠BAC,点P为线段AD上的一个动点,PE⊥AD交BC的延长线于点E.
(1)若∠B=35°,∠ACB=85°,求∠E得度数.
(2)当点P在线段AD上运动时,设∠B=α,∠ACB=β(β>α),求∠E得大小.(用含α、β的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某路公交车从起点经过A、B、C、D站到达终点,一路上下乘客如下表所示。(用正数表示上车的人数,负数表示下车的人数)
| 起点 | A | B | C | D | 终点 |
上车的人数 | 18 | 15 | 12 | 7 | 5 | 0 |
下车的人数 | 0 | -3 | -4 | -10 | -11 |
(1)到终点下车还有_________ 人;
(2)车行驶在那两站之间车上的乘客最多?_______站和________站;
(3)若每人乘坐一站需买票1元,问该车出车一次能收入多少钱?写出算式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,第一个图形是一个六边形,第二个图形是两个六边形组成,依此类推:

(1)写出第n个图形的顶点数(n是正整数);
(2)第12个图有几个顶点?
(3)若有122个顶点,那么它是第几个图形
查看答案和解析>>
科目:初中数学 来源: 题型:
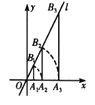
【题目】如图,点![]() 的坐标为
的坐标为![]() ,过点
,过点![]() 作不轴的垂线交直
作不轴的垂线交直![]() 于点
于点![]() 以原点
以原点![]() 为圆心,
为圆心,![]() 的长为半径断弧交
的长为半径断弧交![]() 轴正半轴于点
轴正半轴于点![]() ;再过点
;再过点![]() 作
作![]() 轴的垂线交直线
轴的垂线交直线![]() 于点
于点![]() ,以原点
,以原点![]() 为圆心,以
为圆心,以![]() 的长为半径画弧交
的长为半径画弧交![]() 轴正半轴于点
轴正半轴于点![]() ;…按此作法进行下去,则
;…按此作法进行下去,则![]() 的长是____________.
的长是____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
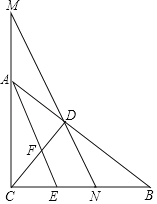
【题目】如图,Rt△ABC中,∠ACB=90°,斜边AB边上的高CD与角平分线AE交于点F,经过垂足D的直线分别交直线CA,BC于点M,N.
(1)若AC=3,BC=4,AB=5,求CD的长;
(2)当∠AMN=32°,∠B=38°时,求∠MDB的度数;
(3)当∠AMN=∠BDN时,写出图中所有与∠CDN相等的角,并选择其中一组进行证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com