
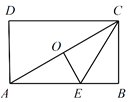
【题目】如图,点![]() 是矩形
是矩形![]() 两条对角线的交点,E是边
两条对角线的交点,E是边![]() 上的点,沿
上的点,沿![]() 折叠后,点
折叠后,点![]() 恰好与点
恰好与点![]() 重合.若
重合.若![]() ,则折痕
,则折痕![]() 的长为 ( )
的长为 ( )
A. ![]() B.
B. ![]() C.
C. ![]() D. 6
D. 6
【答案】A
【解析】
由矩形的性质可得OA=OC,根据折叠的性质可得OC=BC,∠COE=∠B=90°,即可得出BC=![]() AC,OE是AC的垂直平分线,可得∠BAC=30°,根据垂直平分线的性质可得CE=AE,根据等腰三角形的性质可得∠OCE=∠BAC=30°,在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
AC,OE是AC的垂直平分线,可得∠BAC=30°,根据垂直平分线的性质可得CE=AE,根据等腰三角形的性质可得∠OCE=∠BAC=30°,在Rt△OCE中利用含30°角的直角三角形的性质即可求出CE的长.
∵点O是矩形ABCD两条对角线的交点,
∴OA=OC,
∵沿CE折叠后,点B恰好与点O重合.BC=3,
∴OC=BC=3,∠COE=∠B=90°,
∴AC=2BC=6,OE是AC的垂直平分线,
∴AE=CE,
∵∠B=90°,BC=![]() AC,
AC,
∴∠BAC=30°,
∴∠OCE=∠BAC=30°,
∴OC=![]() CE,
CE,
∴CE=2![]() .
.
故选A.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:初中数学 来源: 题型:
【题目】长江中下游地区特大旱情发生后,全国人民抗旱救灾,众志成城.市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节省运费,温州市政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,0是坐标原点,点A坐标为(2, 0),点B坐标为(0, b) (b>0), 点P是直线AB上位于第二象限内的一个动点,过点P作PC垂直于x轴于点C,记点P关于y轴的对称点为Q.
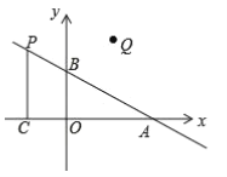
(1)当b=1时:①求直线AB相应的函数表达式:②若![]() ,求点P的坐标:
,求点P的坐标:
(2)设点P的横坐标为a,是否同时存在a、b,使得![]() 是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
是等腰直角三角形?若存在,求出所有满足条件的a、b的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】垫球是排球运动的一项重要技术.下列图表中的数据分别是甲、乙、内三个运动员十次垫球测试的成绩,规则为每次测试连续垫球10个,每垫球到位1个记1分.
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
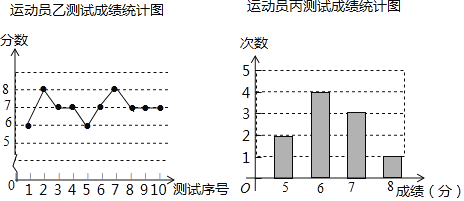
(1)写出运动员甲测试成绩的众数和中位数;
(2)试从平均数和方差两个角度综合分析,若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?(参考数据:三人成绩的方差分别为S甲2=0.8、S乙2=0.4、s丙2=0.81)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】科技发展,社会进步,中国已进入特色社会主义新时代,为实现“两个一百年”奋斗目标和中华民族伟大复兴的中国梦,需要人人奋斗,青少年时期是良好品格形成和知识积累的黄金时期,为此,大数据平台针对部分中学生品格表现和学习状况进行调查统计绘制如下统计图表,请根据图中提供的信息解决下列问题,类别:![]() 品格健全,成绩优异;
品格健全,成绩优异;![]() 尊敬师长,积极进取;
尊敬师长,积极进取;![]() 自控力差,被动学习;
自控力差,被动学习;![]() 沉迷奢玩,消极自卑.
沉迷奢玩,消极自卑.
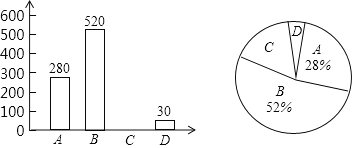
(1)本次调查被抽取的样本容量为 ;
(2)“自控力差,被动学习”的同学有 人,并补全条形统计图;
(3)样本中![]() 类所在扇形的圆心角为 度;
类所在扇形的圆心角为 度;
(4)东至县城内某中学有在校学生3330人,请估算该校![]() 类学生人数.
类学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:数轴上有![]() 、
、![]() 两点,分别对应的数为
两点,分别对应的数为![]() ,
,![]() ,已知
,已知![]() 与
与![]() 互为相反数,点
互为相反数,点![]() 为数轴上一动点,对应为
为数轴上一动点,对应为![]() .
.
(1)若点![]() 到点
到点![]() 和点
和点![]() 的距离相等,求点
的距离相等,求点![]() 对应的数;
对应的数;
(2)数轴上是否存在点![]() ,使点
,使点![]() 到点
到点![]() 和点
和点![]() 的距离之和为5?若存在,请求出
的距离之和为5?若存在,请求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
(3)当点![]() 以每分钟1个单位长度的速度从
以每分钟1个单位长度的速度从![]() 点向左运动,点
点向左运动,点![]() 以每分钟5个单位长度向左运动,点
以每分钟5个单位长度向左运动,点![]() 以每分钟20个单位长度的速度向左运动,问几分钟时点
以每分钟20个单位长度的速度向左运动,问几分钟时点![]() 到点
到点![]() 、点
、点![]() 的距离相等.
的距离相等.

查看答案和解析>>
科目:初中数学 来源: 题型:
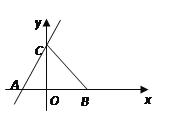
【题目】定义:斜率表示一条直线y=kx+b(k≠0)关于橫坐标轴倾斜程度的量,即直线与x轴正方向夹角(倾斜角α)的正切值,表示成k=tanα。
(1)直线y=x-2b的倾斜角α=________。
(2)如图,在△ABC中,tanA、tanB是方程x2-(![]() +1)x+
+1)x+![]() =0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
=0的两根,且∠A>∠B,B点坐标为(5,0),求出直线AC关系式。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点![]() 在数轴上对应的数为
在数轴上对应的数为![]() ,点
,点![]() 对应的数为
对应的数为![]() ,
,![]() 为原点,且
为原点,且![]() 、
、![]() 满足:
满足:![]() .试解答下列问题:
.试解答下列问题:
(1)求数轴上线段![]() 的长度;
的长度;
(2)若点![]() 以每秒2个单位长度的速度沿数轴向右运动,则经过
以每秒2个单位长度的速度沿数轴向右运动,则经过![]() 秒后点
秒后点![]() 表示的数为 ;(用含
表示的数为 ;(用含![]() 的代数式表示)
的代数式表示)
(3)若点![]() ,
,![]() 都以每秒2个单位长度的速度沿数轴向右运动,而点
都以每秒2个单位长度的速度沿数轴向右运动,而点![]() 不动,经过
不动,经过![]() 秒后其中一个点是一条线段的中点,求此时
秒后其中一个点是一条线段的中点,求此时![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
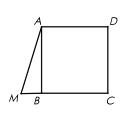
【题目】如图,已知正方形![]() ,点
,点![]() 是线段
是线段![]() 延长线上一点,联结
延长线上一点,联结![]() ,其中
,其中![]() .若将
.若将![]() 绕着点
绕着点![]() 逆时针旋转使得
逆时针旋转使得![]() 与
与![]() 第一次重合时,点
第一次重合时,点![]() 落在点
落在点![]() (图中未画出).求:在此过程中,
(图中未画出).求:在此过程中,
(1)![]() 旋转的角度等于 ______________
旋转的角度等于 ______________![]() .
.
(2)线段![]() 扫过的平面部分的面积为__________(结果保留
扫过的平面部分的面积为__________(结果保留![]() )
)
(3)联结![]() ,则
,则![]() 的面积为____________.
的面积为____________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com