
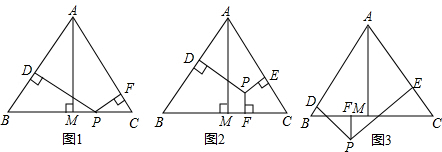
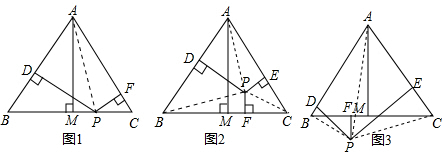
 解:(1)如图1,连接AP,则 S△ABC=S△ABP+S△APC
解:(1)如图1,连接AP,则 S△ABC=S△ABP+S△APC| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
 观察表格:根据表格解答下列问题:
观察表格:根据表格解答下列问题:| x | 0 | 1 | 2 |
| ax | 1 | ||
| ax2+bx+c | -3 | -3 |
查看答案和解析>>
科目:初中数学 来源: 题型:
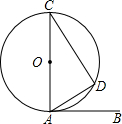 如图,AB与⊙O相切于点A,AC为⊙O的直径,点D在圆上,且满足∠BAD=40°,则∠ACD的大小是( )
如图,AB与⊙O相切于点A,AC为⊙O的直径,点D在圆上,且满足∠BAD=40°,则∠ACD的大小是( )| A、50° | B、45° |
| C、40° | D、42° |
查看答案和解析>>
科目:初中数学 来源: 题型:
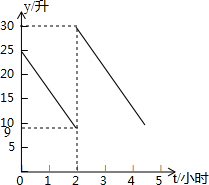 王磊老师驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)的函数关系如图所示.下列说法错误的是( )
王磊老师驾车从甲地到乙地,两地相距500千米,汽车出发前油箱有油25升,途中加油若干升,加油前、后汽车都以100千米/小时的速度匀速行驶,已知油箱中剩余油量y(升)与行驶时间t(小时)的函数关系如图所示.下列说法错误的是( )| A、途中加油21升 |
| B、加油前油箱中剩余油量y(升)与行驶时间t(小时)之间的函数关系是y=-8t+25 |
| C、汽车加油后还可行驶4小时 |
| D、汽车到达乙地时油箱中还余油6升 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com