练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
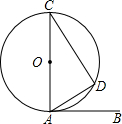
    如图，AB与⊙O相切于点A，AC为⊙O的直径，点D在圆上，且满足∠BAD=40°，则∠ACD的大小是（　　）
    A、50°B、45°
    C、40°D、42°
    考点：切线的性质
    专题：
    分析：根据切线的性质即可得到∠CAB=90°，从而求得∠CAD的度数，然后根据直径所对的圆周角是直角，可证明△ACD是直角三角形，根据直角三角形的性质求解．
    解答：解：∵AB与⊙O相切于点A，
    ∴AC⊥AB，则∠CAB=90°，
    ∴∠CAD=90°-40°=50°，
    又∵AC是⊙O的直径，
    ∴∠ADC=90°，
    ∴∠ACD=90°-∠CAD=90°-50°=40°．
    故选C．
    点评：本题考查了切线的性质以及圆周角定理，注意已知切线时要想到切线垂直于过切点的半径．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    -2x2ym与x2y2是同类项，则m=
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    计算：计算：27
    1
    3
    +(
    		3
    -1)2-(
    1
    2
    )-1+
    4
    		3
    +1
    =
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    已知：等边△ABC和点P，设点P到△ABC的三边AB、AC、BC的距离分别为h1、h2、h3，△ABC的高为h．
    （1）如图1，若点P在边BC上，证明：h1+h2=h．
    （2）如图2，当点P在△ABC内时，猜想h1、h2、h3和h有什么关系？并证明你的结论．
    （3）如图3，当点P在△ABC外时，h1、h2、h3和h有什么关系？（不需要证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    在新年元旦晚会上，九年级二班设置了一个猜谜竞赛，竞赛中成绩处于前两名的同学，分别会获得一次摸球机会，其规则是：在一个口袋中装有4个完全相同的小球，把它们分别标号1、2、3、4，如果摸到1或2，就会赠送相应的礼品，摸到3或4，则无礼品（摸出的球不放回）
    （1）第一位摸球的同学得到奖品的概率是
     
    ；
    （2）小明和小华分别获得一次摸球机会．小明认为先摸比后摸中奖的机会大．小华认为先摸后摸中奖的机会一样大，你同意谁的说法，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    我校组织了安全知识竞赛活动，三个年级根据初赛成绩分别选出了10名同学参加决赛（满分为100分），成绩如下表所示：
    决赛成绩（单位：分）
    七年级80  86  88  80  88  99  80  74  91  89
    八年级85  85  87  97  85  76  88  77  87  88
    九年级82  80  78  78  81  96  97  88  89  86
    （1）请你填表：
    平均数众数中位数
      七年级85.5
     
    		87
      八年级85.585
     
      九年级
     
     
    		84
    （2）请从以下两个不同的角度对三个年级的决赛成绩进行分析：
    ①从平均数和众数相结合看（分析哪个年级成绩好些）：
     
    ；
    ②从平均数和中位数相结合看（分析哪个年级成绩好些）：
     
    ．
    （3）如果在每个年级参加决赛的选手中分别选出3人参加总决赛，你认为哪个年级的实力更强一些．请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

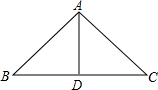    如图，在△ABC中，AB=AC，∠BAC=90°，AD⊥BC，则下列结论不正确的是（　　）
    A、∠BAD=45°
    B、△ABD≌△ACD
    C、AD=
    1
    2
    BC
    D、AD=
    1
    2
    AB

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    梯形中位线长为6，下底长是9，则它的上底长为
     
    ．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    sin245°+tan60°cos30°-tan45°=
     
    ．

    查看答案和解析>>

    同步练习册答案