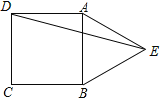
【题目】如图，等边△ABE与正方形ABCD有一条共公边，点E在正方形外，连结DE，则∠BED= °．
【答案】45°
【解析】
试题分析：根据正方形的性质，可得AB与AD的关系，∠BAD的度数，根据等边三角形的性质，可得AE与AB的关系，∠AEB的度数，根据等腰三角形的性质，可得∠AED与∠ADE的关系，根据三角形的内角和，可得∠AED的度数，根据角的和差，可得答案．
解：∵四边形ABCD是正方形，
∴AB=AD，∠BAD=90°，
∵等边三角形ABE，
∴AB=AE，∠BAE=∠AEB=60°，
∠DAE=∠BAD+∠BAE=90°+60°=150°，
AD=AE，
∴∠AEB=∠ABE=（180°﹣∠DAB）÷2=15°，
∴∠BED=∠AEB﹣∠AED=60°﹣15°=45°，
故答案为：45°
口算能手系列答案科目：初中数学 来源： 题型：
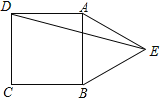
【题目】如图，点E、F分别是ABCD的边BC、AD上的点，且BE=DF．
（1）试判断四边形AECF的形状；
（2）若AE=BE，∠BAC=90°，求证：四边形AECF是菱形．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：如图，AB是⊙O的弦，∠OAB=45°，C是优弧AB上的一点，BD∥OA，交CA延长线于点D，连接BC．
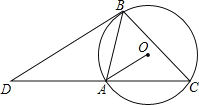
（1）求证：BD是⊙O的切线；
（2）若AC=
，∠CAB=75°，求⊙O的半径．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图1是“东方之星”救援打捞现场图，小红据此构造出一个如图2所示的数学模型，已知：A、B、D三点在同一水平线上，CD⊥AD，∠A=30°，∠CBD=75°，AB=60m．
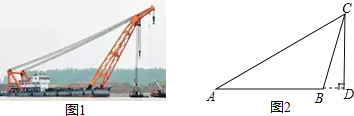
（1）求点B到AC的距离；
（2）求线段CD的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，正方形ABCD的边长为4，点P为对角线BD上一动点，点E在射线BC上．
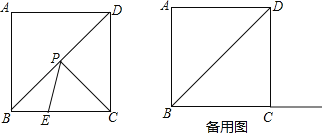
（1）填空：∠PBC= 度．
（2）若BE=t，连结PE、PC，则|PE+PC的最小值为 ，|PE﹣PC|的最大值是 （用含t的代数式表示）；
（3）若点E 是直线AP与射线BC的交点，当△PCE为等腰三角形时，求∠PEC的度数．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com