
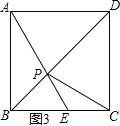
【题目】如图,正方形ABCD的边长为4,点P为对角线BD上一动点,点E在射线BC上.
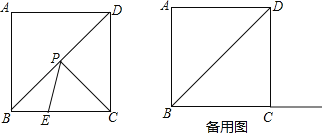
(1)填空:∠PBC= 度.
(2)若BE=t,连结PE、PC,则|PE+PC的最小值为 ,|PE﹣PC|的最大值是 (用含t的代数式表示);
(3)若点E 是直线AP与射线BC的交点,当△PCE为等腰三角形时,求∠PEC的度数.
【答案】(1)45;(2)![]() ;|4﹣t|;(3)当△PCE为等腰三角形时,∠PEC的度数为30°或120°.
;|4﹣t|;(3)当△PCE为等腰三角形时,∠PEC的度数为30°或120°.
【解析】
试题分析:(1)根据正方形的对角线平分一组对角,且四个角为直角,确定出所求角度数即可;
(2)连接AP,当AP与PE在一条线上时,PE+PC最小,利用勾股定理求出最小值;当P与B重合时,|PE﹣PC|最大,表示出最大值即可;
(3)分两种情况考虑:①当E在BC延长线上时,如图2所示,△PCE为等腰三角形,则CP=CE;②当E在BC上,如图3所示,△PCE是等腰三角形,则PE=CE,分别求出∠PEC的度数即可.
解:(1)∠PBC=45度;
故答案为:45;
(2)如图1所示:当AP与PE在一条线上时,PE+PC最小,
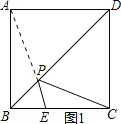
∵AB=4,BE=t,
∴PE+PC的最小值为![]() ;
;
当P与B重合时,|PE﹣PC|的最大值,最大值是|4﹣t|;
故答案为:![]() ;|4﹣t|;
;|4﹣t|;
(3)分两种情况考虑:
①当点E在BC的延长线上时,
如图2所示,△PCE是等腰三角形,则CP=CE,
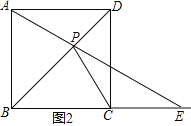
∴∠CPE=∠CEP,
∴∠BCP=∠CPE+∠CEP=2∠CEP,
∵在正方形ABCD中,∠ABC=90°,
∴∠PBA=∠PBC=45°,
在△ABP和△CBP中,
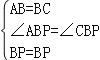 ,
,
∴△ABP≌△CBP(SAS),
∴∠BAP=∠BCP=2∠CEP,
∵∠BAP+∠PEC=90°,
∴2∠PEC+∠PEC=90°,
∴∠PEC=30°;
②当点E在BC上时,
如图3所示,△PCE是等腰三角形,则PE=CE,
∴∠CPE=∠PCE,
∴∠BEP=∠CPE+∠PCE=2∠ECP,
∵四边形ABCD是正方形,
∴∠PBA=∠PBC=45°,
又AB=BC,BP=BP,
∴△ABP≌△CBP,
∴∠BAP=∠BCP,
∵∠BAP+∠AEB=90°,
∴2∠BCP+∠BCP=90°,
∴∠BCP=30°,
∴∠AEB=60°,
∴∠PEC=180°﹣∠AEB=120°,
综上所述:当△PCE为等腰三角形时,∠PEC的度数为30°或120°.


科目:初中数学 来源: 题型:
【题目】图①是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图②的形状拼成一个正方形.
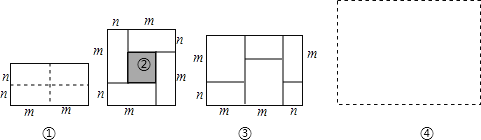
(1)请用两种不同的方法求图②中阴影部分的面积.
方法1:
方法2:
请你写出下列三个代数式: ![]() 之间的等量关系.
之间的等量关系.
;
(2)根据(1)题中的等量关系,解决如下问题:
已知: ![]() 则
则![]() =
=
(3)实际上有许多代数恒等式可以用图形的面积来表示.如图③,它表示的代数恒等式是___ .
(4)已知等式: ![]() ,请你在图④中画出一个相应的几何图形。
,请你在图④中画出一个相应的几何图形。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮家与姥姥家相距24km,小亮8:00从家出发,骑自行车去姥姥家.妈妈8:30从家出发,乘车沿相同路线去姥姥家.在同一直角坐标系中,小亮和妈妈的行进路程S(km)与北京时间t(时)的函数图象如图所示.根据图象得到小亮结论,其中错误的是( )
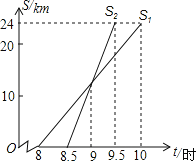
A.小亮骑自行车的平均速度是12km/h
B.妈妈比小亮提前0.5小时到达姥姥家
C.妈妈在距家12km处追上小亮
D.9:30妈妈追上小亮
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个口袋里有四个完全相同的小球,把它们分别标号为1,2,3,4,小明和小强采取的摸取方法分别是:
小明:随机摸取一个小球记下标号,然后放回,再随机摸取一个小球,记下标号;
小强:随机摸取一个小球记下标号,不放回,再随机摸取一个小球,记下标号.
(1)用画树状图(或列表法)分别表示小明和小强摸球的所有可能出现的结果;
(2)分别求出小明和小强两次摸球的标号之和等于5的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用白铁皮做罐头盒,每张铁片可制盒身16个或制盒底43个,一个盒身与两个盒底配成一套罐头盒,现有150张白铁皮,用多少张制盒身,多少张制盒底,可以正好制成整套罐头盒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com