
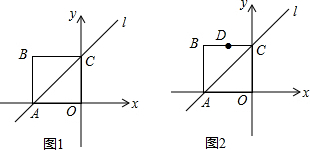
���� ��1����ͼ1�У����ֱ��l�Ľ���ʽΪy=x+2�����P������Ϊ��m��m+2�����������$\frac{1}{2}$��2��|m+2|=3���ⷽ�̼��ɣ�
��2����ͼ2�У�����OD��ֱ��l�ڵ�E�����EΪ����ʱ|BE+DE|=|OE+DE|=OD��OD��Ϊ���ֵ�����ֱ��OD�Ľ���ʽ�����÷����������E���꼴�ɣ�
��3����ͼ3�У�O��B����ֱ��l�Գƣ�����BE=OE��|BE-DE|=|OE-DE|��������֮��С�ڵ�����֪������O��D��E���㹲��ʱ��|OE-DE|��ֵ������ֵΪOD�����ֱ��OD�Ľ���ʽ�����÷������������E���꼴�ɣ�
��� �⣺��1����ͼ1�У�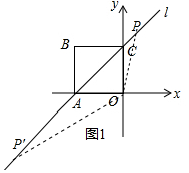
������֪��A����C������ֱ�Ϊ��-2��0���ͣ�0��2��
��ֱ��l�ĺ�������ʽy=kx+b��k��0����������A��-2��0���͵�C��0��2����
��$\left\{\begin{array}{l}{-2k+b=0}\\{b=2}\end{array}\right.$���$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$��
��ֱ��l�Ľ���ʽΪy=x+2��
���P��������m��m+2����
�������$\frac{1}{2}$��2��|m+2|=3����m=1��m=-5��
��P��1��3����P�䣨-5��-3����
��2����ͼ2�У�����OD��ֱ��l�ڵ�E�����EΪ����ʱ|BE+DE|=|OE+DE|=OD��OD��Ϊ���ֵ��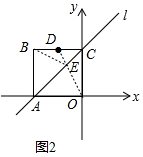
��OD����ֱ��Ϊy=k1x��k1��0����������D��-1��2����
��2=-k1��
��k1=-2��
��ֱ��ODΪy=-2x��
��$\left\{\begin{array}{l}{y=x+2}\\{y=-2x}\end{array}\right.$ ���$\left\{\begin{array}{l}{x=-\frac{2}{3}}\\{y=\frac{4}{3}}\end{array}\right.$��
���E��������-$\frac{2}{3}$��$\frac{4}{3}$����
�֡ߵ�D������Ϊ��-1��2����
���ɹ��ɶ����ɵ�OD=$\sqrt{5}$��
��|BE+DE|����СֵΪ$\sqrt{5}$��
��3����ͼ3�У�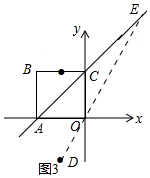
��O��B����ֱ��l�Գƣ�
��BE=OE����|BE-DE|=|OE-DE|��
������֮��С�ڵ�����֪������O��D��E���㹲��ʱ��|OE-DE|��ֵ������ֵΪOD��
��D��-1��-2����
��ֱ��OD�Ľ���ʽΪy=2x��OD=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$��
��$\left\{\begin{array}{l}{y=2x}\\{y=x+2}\end{array}\right.$�����$\left\{\begin{array}{l}{x=2}\\{y=4}\end{array}\right.$��
���E��2��4����
��|BE-D��E|�����ֵΪ$\sqrt{5}$��ʱ��E������Ϊ��2��4����
���� ���⿼���ı����ۺ��⡢һ�κ�����Ӧ�á������ε����ʡ������ε���������ɶ�����֪ʶ������Ĺؼ���ѧ�����öԳƣ���������֮���߶���̣������Сֵ���⣬���������ε�����֮��С�ڵ����ߣ�ȷ�����ֵ���⣬�����п��������ͣ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
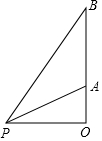 ��ͼ��һö����ӵ���O�����䣬�ھ��뷢���9km���ĵ���۲�վP���û���ײ�����A��ʱ����ײ�������Ϊ30�㣻20s�����ײ�����B�㣬�����ײ�������Ϊ60�㣮����ö�����A�㵽B���ƽ���ٶȣ���ȷ�� 0.1km/s�����ο����ݣ�$\sqrt{2}$��1.41��$\sqrt{3}$��1.73��$\sqrt{5}$��2.24��
��ͼ��һö����ӵ���O�����䣬�ھ��뷢���9km���ĵ���۲�վP���û���ײ�����A��ʱ����ײ�������Ϊ30�㣻20s�����ײ�����B�㣬�����ײ�������Ϊ60�㣮����ö�����A�㵽B���ƽ���ٶȣ���ȷ�� 0.1km/s�����ο����ݣ�$\sqrt{2}$��1.41��$\sqrt{3}$��1.73��$\sqrt{5}$��2.24���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
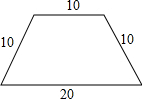 ��һ��Χ�����ε���ʣ����ĸ��߳���ͼ��ʾ��Ϊ�������ô���������Χ��һ����������ʣ�ʹ��Χ�ɵij����ε�һ�߳�Ϊ10�����ʱ���Χ�ɵij����ε���һ�߳�Ϊ���٣�����Χ��һ�������ε���ʣ������εı߳�Ϊ���٣����Ƚ�Χ���ij����κ��������ĸ��������
��һ��Χ�����ε���ʣ����ĸ��߳���ͼ��ʾ��Ϊ�������ô���������Χ��һ����������ʣ�ʹ��Χ�ɵij����ε�һ�߳�Ϊ10�����ʱ���Χ�ɵij����ε���һ�߳�Ϊ���٣�����Χ��һ�������ε���ʣ������εı߳�Ϊ���٣����Ƚ�Χ���ij����κ��������ĸ���������鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com