
甲、乙两车分别从A,B两地同时出发相向而行.并以各自的速度匀速行驶,甲车途径C地时休息一小时,然后按原速度继续前进到达B地;乙车从B地直接到达A地,如图是甲、乙两车和B地的距离y(千米)与甲车出发时间x(小时)的函数图象.
(1)直接写出a,m,n的值;
(2)求出甲车与B地的距离y(千米)与甲车出发时间x(小时)的函数关系式(写出自变量x的取值范围);
(3)当两车相距120千米时,乙车行驶了多长时间?
(1)a=90,m=1.5,n=3.5。
(2)y与x的关系式为
(3)乙车行驶了1小时或3小时
解析试题分析:(1)∵甲车途径C地时休息一小时,∴2.5﹣m=1。∴m=1.5。
∵乙车的速度为: ,即
,即 ,解得a=90。
,解得a=90。
甲车的速度为: ,解得n=3.5。
,解得n=3.5。
∴a=90,m=1.5,n=3.5。
(2)分休息前,休息时,休息后三个阶段,利用待定系数法求一次函数解析式解答。
(3)求出甲车的速度,然后分①相遇前两人的路程之和加上相距的120千米等于总路程列出方程求解即可;②相遇后,两人行驶的路程之和等于总路程加120千米,列出方程求解即可。
解:(1)a=90,m=1.5,n=3.5。
(2)设甲车的y与x的函数关系式为y=kx+b(k≠0),
①休息前,0≤x<1.5,函数图象经过点(0,300)和(1.5,120),
∴ ,解得
,解得 。
。
∴y=﹣120x+300,
②休息时,1.5≤x<2.5,y=120。
③休息后,2.5≤x≤3.5,函数图象经过(2.5,120)和(3.5,0),
所以, ,解得
,解得 。
。
∴y=﹣120x+420。
综上所述,y与x的关系式为 。
。
(3)设两车相距120千米时,乙车行驶了x小时,甲车的速度为:(300﹣120)÷1.5=120千米/时。
①若相遇前,则120x+60x=300﹣120,解得x=1。
②若相遇后,则120(x﹣1)+60x=300+120,解得x=3。
∴两车相距120千米时,乙车行驶了1小时或3小时。


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
已知:如图,反比例函数的图象经过点A、B,点A的坐标为(1,3),点B的纵坐标为1,点C的坐标为(2,0).
(1)求该反比例函数的解析式;
(2)求直线BC的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
为了响应国家节能减排的号召,鼓励市民节约用电,我市从2012年7月1日起,居民用电实行“一户一表”的“阶梯电价”,分三个档次收费,第一档是用电量不超过180千瓦时实行“基本电价”,第二、三档实行“提高电价”,具体收费情况如右折线图,请根据图象回答下列问题;
(1)当用电量是180千瓦时时,电费是 元;
(2)第二档的用电量范围是 ;
(3)“基本电价”是 元/千瓦时;
(4)小明家8月份的电费是328.5元,这个月他家用电多少千瓦时?
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
某农场的一个家电商场为了响应国家家电下乡的号召,准备用不超过105700元购进40台电脑,其中A型电脑每台进价2500元,B型电脑每台进价2800元,A型每台售价3000元,B型每台售价3200元,预计销售额不低于123200元.设A型电脑购进x台、商场的总利润为y(元).
(1)请你设计出进货方案;
(2)求出总利润y(元)与购进A型电脑x(台)的函数关系式,并利用关系式说明哪种方案的利润最大,最大利润是多少元?
(3)商场准备拿出(2)中的最大利润的一部分再次购进A型和B型电脑至少各两台,另一部分为地震灾区购买单价为500元的帐篷若干顶.在钱用尽三样都购买的前提下请直接写出购买A型电脑、B型电脑和帐篷的方案.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
学校准备购买一批乒乓球桌.现有甲、乙两家商店卖价如下:甲商店:每张需要700元.乙商店:交1000元会员费后,每张需要600元.设学校需要乒乓球桌x张,在甲商店买和在乙商店买所需费用分别为y1、y2元.
(1)分别写出y1、y2的函数解析式.
(2)当学校添置多少张时,两种方案的费用相同?
(3)若学校需要添置乒乓球桌20张,那么在那个商店买较省钱?说说你的理由.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
如图,反比例函数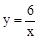 的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
的图象与一次函数y=kx+b的图象相交于两点A(m,3)和B(﹣3,n).
(1)求一次函数的表达式;
(2)观察图象,直接写出使反比例函数值大于一次函数值的自变量x的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com