
����Ŀ����һ�鳤18�ף���15�ľ��λĵ�����һ��������Ӱ���֣���ռ�����Ϊԭ���ĵ����������֮��������ȷ��0.1m��
��1����Ʒ���1����ͼ1���������������ഹֱ�ҿ�����ȵ�С·��
��2����Ʒ���2����ͼ2������ÿ���ǵ����ζ���ͬ��
�������ַ����Ƿ��ܷ�������?���ܣ�������ͼ���е�С·�Ŀ���ͼ�������εİ뾶�������ܷ�����������˵�����ɣ�

���𰸡�����.С·�Ŀ�ԼΪ6.6m�����ΰ뾶ԼΪ7.6m.
�������������������1����С·��Ϊxm��������Ӱ������ռ�����Ϊ�������������֮������һԪ���η��̣����˷����н⣬˵���˷���������������˷�����⣬��������������2�������ΰ뾶Ϊrm����Ϊÿ���ǵ����κ�������һ��Բ��������Բ��������ھ������������֮������һԪ���η��̣����˷����н⣬˵���˷���������������˷�����⣬������������
�����������1����С·��Ϊx��������Ӱ������ռ�����Ϊ�������������֮������һԪ���η��̣���18x+16x��x2=![]() ��18��15��������x2��34x+180=0����������̣���x=
��18��15��������x2��34x+180=0����������̣���x=![]() ��x=
��x=![]() ������������ȥ���� x=
������������ȥ���� x=![]() ��6.6.����С·�Ŀ�ԼΪ6.6m����2�������ΰ뾶Ϊr����Ϊÿ���ǵ����κ�������һ��Բ��������Բ��������ھ������������֮������һԪ���η��̣���3.14r2=
��6.6.����С·�Ŀ�ԼΪ6.6m����2�������ΰ뾶Ϊr����Ϊÿ���ǵ����κ�������һ��Բ��������Բ��������ھ������������֮������һԪ���η��̣���3.14r2=![]() ��18��15�����r2��57.32����ֵ��ȥ������r��7.6.�������ΰ뾶ԼΪ7.6m.
��18��15�����r2��57.32����ֵ��ȥ������r��7.6.�������ΰ뾶ԼΪ7.6m.


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ʒ���ɱ������20%��ۣ�Ȼ���9�۳��ۣ���ʱ�Կɻ���16Ԫ������Ʒ�ijɱ���Ϊ Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ���п����Ȱ��ɱ������50%��ۣ��ٽ���۴�8�۳��ۣ��������28Ԫ�����������п����ijɱ�����xԪ����ô�������⣬���з�����ȷ���ǣ�������
A.0.8��1+0.5��x=x+28
B.0.8��1+0.5��x=x��28
C.0.8��1+0.5x��=x��28
D.0.8��1+0.5x��=x+28
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ���ı���ABCD�У�����A��AE��BC������ΪE������DE��FΪ�߶�DE��һ�㣬�ҡ�AFE=��B��
��1����֤����ADF�ס�DEC��
��2����AB=4��AD=![]() ��AE=3����AF�ij���
��AE=3����AF�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���A=40������B=70����CEƽ�֡�ACB��CD��AB�ڵ�D��DF��CE�ڵ�F�����CDF�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������İ뾶Ϊ6.4��103km,�����������ȷ���� ��
A. ��λ B. ʮ��λ C. ʮλ D. ��λ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ABC�У���C��90����BC��6 cm��AC��8 cm����P�ӵ�A��ʼ��AC���C��2����/����ٶ��˶������ͬʱ����Q�ӵ�C��ʼ��CB�����B��1����/����ٶ��˶������P��Q�ֱ��A��Cͬʱ������������һ�㵽���յ�ʱ����һ��Ҳ��ֹ֮ͣ�˶���
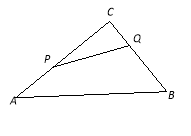
��1���������룬��CPQ���������3cm2?
��2���������˶������У��Ƿ����ijһʱ��t��ʹPQǡ��ƽ����ABC������������ڣ�����˶�ʱ��t���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com