
如图1,在平面直角坐标系中,AB=OB=8,∠ABO=90°,∠yOC=45°,射线OC以每秒2个单位长度的速度向右平行移动,当射线OC经过点B时停止运动,设平行移动x秒后,射线OC扫过Rt△ABO的面积为y.
(1)求y与x之间的函数关系式;
(2)当x=3秒时,射线OC平行移动到O′C′,与OA相交于G,如图2,求经过G,O,B三点的抛物线的解析式;
(3)现有一动点P在(2)中的抛物线上,试问点P在运动过程中,是否存在三角形POB的面积S=8的情况?若存在,求出点P的坐标,若不存在,请说明理由.
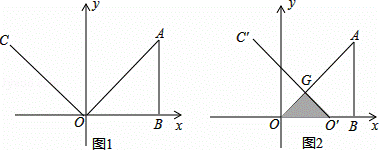


解:(1)∵AB=OB,∠ABO=90°,
∴△ABO是等腰直角三角形,
∴∠AOB=45°,
∵∠yOC=45°,
∴∠AOC=(90°﹣45°)+45°=90°,
∴AO⊥CO,
∵C′O′是CO平移得到,
∴AO⊥C′O′,
∴△OO′G是等腰直角三角形,
∵射线OC的速度是每秒2个单位长度,
∴OO′=2x,
∴y=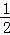 ×(2x)2=2x2;
×(2x)2=2x2;
(2)当x=3秒时,OO′=2×3=6,
∵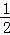 ×6=3,
×6=3,
∴点G的坐标为(3,3),
设抛物线解析式为y=ax2+bx,
则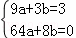 ,
,
解得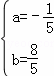 ,
,
∴抛物线的解析式为y=﹣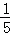 x2+
x2+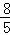 x;
x;
(3)设点P到x轴的距离为h,
则S△POB=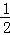 ×8h=8,
×8h=8,
解得h=2,
当点P在x轴上方时,﹣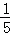 x2+
x2+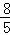 x=2,
x=2,
整理得,x2﹣8x+10=0,
解得x1=4﹣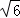 ,x2=4+
,x2=4+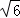 ,
,
此时,点P的坐标为(4﹣ ,2)或(4+
,2)或(4+ ,2);
,2);
当点P在x轴下方时,﹣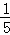 x2+
x2+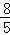 x=﹣2,
x=﹣2,
整理得,x2﹣8x﹣10=0,
解得x1=4﹣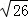 ,x2=4+
,x2=4+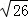 ,
,
此时,点P的坐标为(4﹣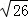 ,﹣2)或(4+
,﹣2)或(4+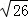 ,﹣2),
,﹣2),
综上所述,点P的坐标为(4﹣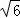 ,2)或(4+
,2)或(4+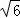 ,2)或(4﹣
,2)或(4﹣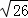 ,﹣2)或(4+
,﹣2)或(4+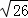 ,﹣2)时,△POB的面积S=8.
,﹣2)时,△POB的面积S=8.



科目:初中数学 来源: 题型:
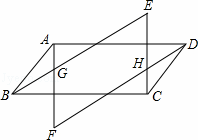
如图,四边形ABCD是平行四边形,作AF∥CE,BE∥DF,AF交BE与G点,交DF与F点,CE交DF于H点、交BE于E点.
求证:△EBC≌△FDA.


查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com