
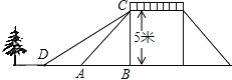
【题目】如图,某公园内有座桥,桥的高度是5米,CB⊥DB,坡面AC的倾斜角为45°,为方便老人过桥,市政部门决定降低坡度,使新坡面DC的坡度为i= ![]() :3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据:
:3.若新坡角外需留下2米宽的人行道,问离原坡角(A点处)6米的一棵树是否需要移栽?(参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)
【答案】不需要移栽,理由见解析
【解析】
根据题意得到三角形ABC为等腰直角三角形,求出AB的长,在直角三角形BCD中,根据新坡面的坡度求出∠BDC的度数为30,利用30度角所对的直角边等于斜边的一半求出DC的长,再利用勾股定理求出DB的长,由DB-AB求出AD的长,然后将AD+2与6进行比较,若大于则需要移栽,反之不需要移栽.
解:不需要移栽,理由为: ∵CB⊥AB,∠CAB=45°,
∴△ABC为等腰直角三角形,
∴AB=BC=5米,
在Rt△BCD中,新坡面DC的坡度为i= ![]() :3,即∠CDB=30°,
:3,即∠CDB=30°,
∴DC=2BC=10米,BD= ![]() BC=5
BC=5 ![]() 米,
米,
∴AD=BD﹣AB=(5 ![]() ﹣5)米≈3.66米,
﹣5)米≈3.66米,
∵2+3.66=5.66<6,
∴不需要移栽.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,函数 y kx 与 y  的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数
的图象交于 A、B 两点,过 A 作 y 轴的垂线,交函数 的图象于点 C,连接 BC,则△ABC 的面积为( )
的图象于点 C,连接 BC,则△ABC 的面积为( )

A. 2 B. 4 C. 6 D. 8
查看答案和解析>>
科目:初中数学 来源: 题型:
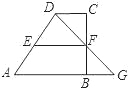
【题目】如图,梯形ABCD中,AB∥CD,点F在BC上,连DF与AB的延长线交于点G.
(1)求证:△CDF∽△BGF;
(2)当点F是BC的中点时,过F作EF∥CD交AD于点E,若AB=6cm,EF=4cm,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,一幢楼房AB背后有一台阶CD,台阶每层高0.2米,且AC=14.5米,NF=0.2米.设太阳光线与水平地面的夹角为α,当α=56.3°时,测得楼房在地面上的影长AE=10米,现有一只小猫睡在台阶的NF这层上晒太阳.

(1)求楼房的高度约为多少米?
(2)过了一会儿,当α=45°时,问小猫能否还晒到太阳?请说明理由.(参考数据:sin56.3°≈0.83,cos56.3°≈0.55,tan56.3°≈1.5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阳光市场某个体商户购进某种电子产品,每个进价是50元.调查发现,当售价是80元时,平均一周可卖出160个,而当售价每降低2元时,平均一周可多卖出20个.若设每个电子产品降价x元,
(1)根据题意,填表:
进价(元) | 售价(元) | 每件利润(元) | 销量(个) | 一周总利润(元) | |
降价前 | 50 | 80 | 30 | 160 |
|
降价后 | 50 |
(2)若商户计划每周盈利5200元,且尽量减少库存,则应降价多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,点A,B的坐标分别为(1,0),(0,2),某抛物线的顶点坐标为D(-1,1)且经过点B,连接AB,直线AB与此抛物线的另一个交点为C,则S△BCD:S△ABO=( )

A. 8:1B. 6:1C. 5:1D. 4:1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=1,与x轴的一个交点坐标为(﹣1,0),其部分图象如图所示,下列结论:①4ac<b2;、②3a+c>0;③当x>0时,y随x的增大而减小;④当y>0时,x的取值范围是﹣1<x<3;⑤方程ax2+bx+c=0的两个根是x1=﹣1,x2=3;其中结论正确的个数是( )
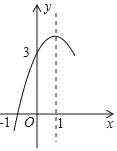
A. 4个 B. 3个 C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
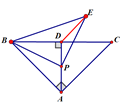
【题目】在Rt△ABC中,∠BAC=90,AB=AC,AD⊥BC于点D,P是线段AD上的一个动点,以点P为直角的顶点,向上作等腰直角三角形PBE,连接DE,若在点P的运动过程中,DE的最小值为3,则AD的长为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AC的垂直平分线EF交AC于点D,交AB于点F,且CE=BF.
(1)求证:四边形AECF是菱形;
(2)当∠BAC的度数为多少时,四边形AECF是正方形.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com