
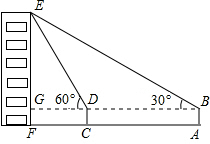
 如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米)
如图,小俊在A处利用高为1.5米的测角仪AB测得楼EF顶部E的仰角为30°,然后前进12米到达C处,又测得楼顶E的仰角为60°,求楼EF的高度.($\sqrt{3}$=1.732,结果精确到0.1米) 分析 根据三角形的外角的性质求出∠DEB=30°,根据等腰三角形的性质求出DE=DB=12米,解Rt△EDG求出EG,根据EF=EG+GF即可求解.
解答 解:∵∠EDG=60°,∠EBG=30°,
∴∠DEB=30°,
∴DE=DB=12米,
在Rt△EDG中,sin∠EDG=$\frac{EG}{ED}$,
∴EG=ED•sin∠EDG=12×$\frac{\sqrt{3}}{2}$=6$\sqrt{3}$,
∴EF=EG+GF=6$\sqrt{3}$+1.5≈11.9,
答:楼EF的高度约为11.9米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角的概念、等腰三角形的性质、熟记锐角三角函数的定义是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
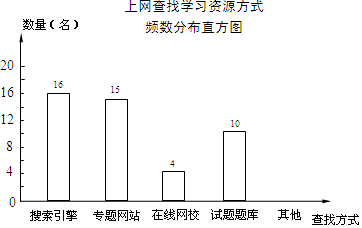 某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.
某学校为了了解本校学生采用何种方式上网查找所需要的学习资源,随机抽取部分学生了解情况,并将统计结果绘制成频数分布表及频数分布直方图.| 查找方式 | 频数 | 频率 |
| 搜索引擎 | 16 | 32% |
| 专题网站 | 15 | a |
| 在线网校 | 4 | 8% |
| 试题题库 | 10 | 20% |
| 其他 | b | 10% |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
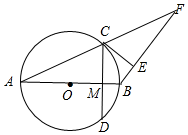 如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.
如图,以AB为直径的⊙O与AF交于C点,过C作CE⊥BF,且CE与⊙O相切,过C作CD⊥AB交AB于M,AB=10,OM:BM=3:2.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
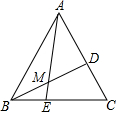 如图,在等边△ABC中,D为AC边上的一点,连接BD,M为BD上一点,且∠AMD=60°,AM交BC于E.当M为BD中点时,$\frac{CD}{AD}$的值为( )
如图,在等边△ABC中,D为AC边上的一点,连接BD,M为BD上一点,且∠AMD=60°,AM交BC于E.当M为BD中点时,$\frac{CD}{AD}$的值为( )| A. | $\frac{2}{3}$ | B. | $\frac{\sqrt{5}-1}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 5×102吨 | B. | 5×106吨 | C. | 5×107吨 | D. | 5×108吨 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com