练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    在Rt△ABC中AC=6，BC=8，则斜边上的中线CD=
     
    ．
    分析：根据勾股定理求出AB，再利用直角三角形中斜边上的中线等于斜边的一半求的CD的长，再利用BC为斜边得出CD的长．
    解答：精英家教网解：Rt△ABC中，∠ACB=90°，当AC=6，BC=8为直角边，
    ∴AB2=AC2+BC2=82+62=100，
    ∴AB=10；
    在Rt△ABC中，CD为斜边AB的中线，
    ∴CD=
    1
    2
    AB（直角三角形斜边上的中线等于斜边的一半），
    ∴CD=5．
    当BC为斜边，则斜边上的中线CD=4，
    故答案是：5或4．
    点评：解答本题主要是运用了直角三角形的性质，即勾股定理和在直角三角形斜边上的中线等于斜边的一半．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    精英家教网在Rt△ABC中AC=6cm，BC=8cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合，求（1）AB的长；（2）CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

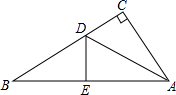    在Rt△ABC中AC=9cm，BC=12cm，现将直角边AC沿直线AD折叠，使它落在斜边AB上，且与AE重合．求：
    （1）AB=
    15
    15
    cm，BE=
    6
    6
    cm；
    （2）设CD=x，则DE=
    x
    x
    cm，BD=
    （12-x）
    （12-x）
    cm；
    （3）求CD的长及△BAD的面积．

    查看答案和解析>>

    科目：初中数学 来源：2011-2012学年浙江省温州四中八年级下学期期中数学试卷（带解析） 题型：解答题

    如图，在Rt△ABC中,AC=AB，∠BAC=90°，点O是BC的中点，连结OA.
    （1）如图1，已知BC=6,则OA=_________.
    （2）如图2，若点M,N分别在线段AB,AC上移动，在移动中始终保持AN=BM，则△OAN≌△OBM成立吗？并说明理由.
    （3）如图3，若点M,N分别在线段BA.AC的延长线上移动，在移动中始终保持AN=BM，请判断△OMN的形状，并说明理由.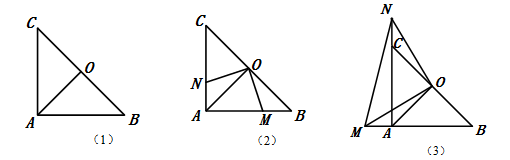

    查看答案和解析>>

    科目：初中数学 来源：2013届浙江省八年级下学期期中数学试卷（解析版） 题型：解答题

    如图，在Rt△ABC中,AC=AB，∠BAC=90°，点O是BC的中点，连结OA.

    （1）如图1，已知BC=6,则OA=_________.

    （2）如图2，若点M,N分别在线段AB,AC上移动，在移动中始终保持AN=BM，则△OAN≌△OBM成立吗？并说明理由.

    （3）如图3，若点M,N分别在线段BA.AC的延长线上移动，在移动中始终保持AN=BM，请判断△OMN的形状，并说明理由.

     

     

     

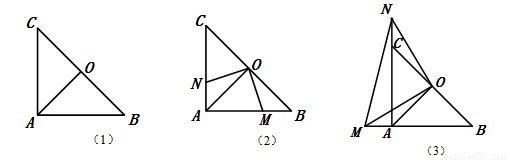
    查看答案和解析>>

    同步练习册答案