
| 城市费用城市 | 海南 | 厦门 |
| 青岛 | 4万/台 | 8万/台 |
| 大连 | 3万/台 | 5万/台 |
| 城市台数城市 | 海南 | 厦门 |
| 青岛 | x | |
| 大连 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 完成下列推理过程
完成下列推理过程查看答案和解析>>
科目:初中数学 来源: 题型:
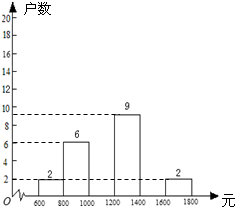 暑假期间,学校布置了综合实践活动任务,王涛小组四人负责调查本村的500户农民的家庭收入情况,他们随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并制定了频数分布表和频数分布直方图.
暑假期间,学校布置了综合实践活动任务,王涛小组四人负责调查本村的500户农民的家庭收入情况,他们随机调查了40户居民家庭的收入情况(收入取整数,单位:元),并制定了频数分布表和频数分布直方图.| 分组 | 频数 | 百分比 |
| 600≤x<800 | 2 | 5% |
| 800≤x<1000 | 6 | 15% |
| 1000≤x<1200 | 45% | |
| 1200≤x<1400 | 9 | 22.5% |
| 1400≤x<1600 | ||
| 1600≤x<1800 | 2 | 5% |
| 合计 | 40 | 100% |
查看答案和解析>>
科目:初中数学 来源: 题型:
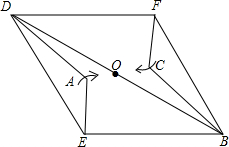 如图,已知:?ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形.
如图,已知:?ABCD的对角线交点为O,点E、F分别在边AB、CD上,分别沿DE、BF折叠四边形ABCD,A、C两点恰好都落在O点处,且四边形DEBF为菱形.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com