

分析 (1)在Rt△ABC中,根据∠ACB=90°,AB=10,BC=8,由勾股定理可得AC的长;
(2)由题意可知AD=2t,当AB=AD时,有2t=10;当AB=BD时,则可知AC=CD,则AD=12,即2t=12;当AD=BD时,CD=2t-6,BD=2t,在Rt△BDC中,由勾股定理可得BC2+CD2=BD2,可得到关于t的方程,分别求得t即可;
(3)分情况讨论:当点D与点C重合时,∠BCA'=90°,此时△A′BC为直角三角形;当A'B∥AC时,∠CBA'=∠ACB=90°,此时△A′BC为直角三角形,分别求得t的值即可.
解答 解:(1)如图1,
在Rt△ABC中,∠ACB=90°,AB=10,BC=8,
∴由勾股定理得,AC=$\sqrt{A{B}^{2}-B{C}^{2}}$=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∴AC的长度为6;
(2)如图2,动点D从点A出发沿射线AC方向以每秒2个单位的速度运动,点D运动的时间为t(t>0)秒,
∴AD=2t,
①当AB=AD时,有2t=10,
解得t=5;
②当AB=BD时,根据BC⊥AD可知AC=CD,
∴AD=12,即2t=12,
解得t=6;
③当AD=BD=2t时,CD=2t-6,
在Rt△BDC中,由勾股定理可得,BC2+CD2=BD2,
即64+(2t-6)2=4t2,
解得t=$\frac{25}{6}$;
综上所述,t的值为5s或6s或$\frac{25}{6}$s时,△ABD是等腰三角形;
(3)如图3所示,当点D与点C重合时,∠BCA'=90°,此时△A′BC为直角三角形,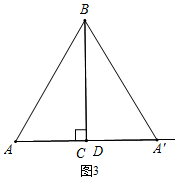
∴AC=AD=6,
∴t=6÷2=3(s);
如图4所示,当A'B∥AC时,∠CBA'=∠ACB=90°,此时△A′BC为直角三角形,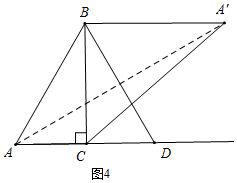
连接AA',则AA'被BD垂直平分,
∴BA=BA',
∵BD⊥AA',
∴∠ABD=∠A'BD,
又∵A'B∥AD,
∴∠ADB=∠A'BD,
∴∠ADB=∠ABD,
∴AB=AD=10,
∴t=10÷2=5(s).
∵∠BA'C<∠BAC<90°,
∴∠BA'C不可能是直角.
综上所述,当△A′BC为直角三角形时,t的值为3或5秒.
点评 本题以动点问题为背景,主要考查了直角三角形的性质,等腰三角形的性质与判定以及轴对称的性质的综合应用,解决问题的关键是运用分类思想进行讨论,在分类时注意不能遗漏,也不能重复.解题时注意:如果两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:解答题
| 档次 | 月用电量 | 电价(单位:元/度) |
| 第1档 | 月用电量≤200度 | 0.5 |
| 第2档 | 200度<月用电量≤400度 | 0.55 |
| 第3档 | 月用电量>400度 | 0.8 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.
如图,已知直线l经过点A(4,0)和B(0,-4),它与抛物线y=ax2在第三象限内相交于点P,如果△AOP的面积为$\frac{19}{2}$,求a的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
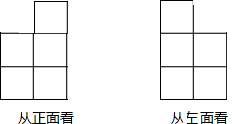 用小立方块搭一个几何体,使得从它的正面和左面看到的形状如图所示.
用小立方块搭一个几何体,使得从它的正面和左面看到的形状如图所示.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com