
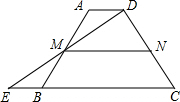
 如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.
如图,在梯形ABCD中,AD∥BC,延长CB到点E,使BE=AD,连接DE交AB于点M.分析 (1)找出全等的条件:BE=AD,∠A=∠ABE,∠E=∠ADE,即可证明;
(2)首先证得MN是三角形的中位线,根据MN=$\frac{1}{2}$(BE+BC),又BE=2,即可求得.
(3)结论:MN=$\frac{1}{2}$(AD+BC)
解答 (1)证明:∵AD∥BC,
∴∠A=∠MBE,∠ADM=∠E,
在△AMD和△BME中,
$\left\{\begin{array}{l}{∠A=∠MBE}\\{AD=BE}\\{∠ADM=∠E}\end{array}\right.$,
∴△AMD≌△BME(ASA);
(2)解:∵△AMD≌△BME,
∴MD=ME,ND=NC,
∴MN=$\frac{1}{2}$EC,
∴EC=2MN=2×5=10,
∴BC=EC-EB=10-2=8.
答:BC的长是8.
(3)结论:MN=$\frac{1}{2}$(AD+BC).
点评 本题考查了全等三角形的判断及三角形中位线定理的应用,熟记其性质、定理是证明、解答的基础.


 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 一个有理数,如果它不是正数,那么它一定是负数 | |
| B. | a的倒数是$\frac{1}{a}$ | |
| C. | 若盈利26元记作+26元,则亏损68元记作-68元 | |
| D. | 绝对值等于它本身的数是l |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
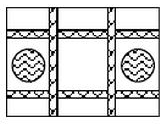 “G20峰会“将于2016年9月在抗州举行,杭州迸进行全面撤城市美化工程.小丽爸爸是一个园林设计师.将对一块长80m,宽60m的空地进行园艺设计(如图),在空地设计两纵两横相同宽度的小路,再设计两个半径为路宽2倍的圆形喷水池,喷水池和小路的面积之和占整个空地面积的$\frac{2}{15}$.
“G20峰会“将于2016年9月在抗州举行,杭州迸进行全面撤城市美化工程.小丽爸爸是一个园林设计师.将对一块长80m,宽60m的空地进行园艺设计(如图),在空地设计两纵两横相同宽度的小路,再设计两个半径为路宽2倍的圆形喷水池,喷水池和小路的面积之和占整个空地面积的$\frac{2}{15}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
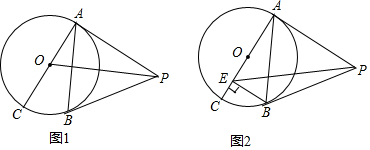 已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.
已知PA,PB与⊙O分别相切于点A,B,AC是⊙O的直径.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
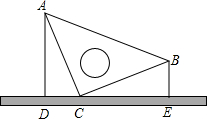 如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )
如图,桌面上竖直放置一等腰直角三角板ABC,若测得斜边AB在桌面上的投影DE为8cm,且点B距离桌面的高度为3cm,则点A距离桌面的高度为( )| A. | 6.5cm | B. | 5cm | C. | 9.5cm | D. | 11cm |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
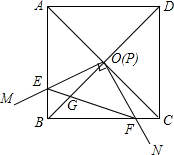 如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )
如图,边长为1的正方形ABCD的对角线AC,BD相交于点O,∠MPN为直角,使点P与点O重合,直角边PM,PN分别与OA,OB重合,然后逆时针旋转∠MPN,旋转角为θ(0°<θ<90°),PM,PN分别交AB,BC于E,F两点,连接EF交OB于点G,则下列结论:①EF=$\sqrt{2}$OE;②S四边形OEBF:S正方形ABCD=1:4;③BE+BF=$\sqrt{2}$OA;④在旋转过程中,当△BEF与△COF的面积之和最大时,AE=$\frac{3}{4}$;⑤OG•BD=AE2+CF2.其中结论正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com