Question

17．问题提出：如图1，在Rt△ABC中，∠ACB=90°，CB=4，CA=6，⊙C半径为2，P为圆上一动点，连结AP、BP，求AP+$\frac{1}{2}$BP的最小值．
（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD=1，则有$\frac{CD}{CP}$=$\frac{CP}{CB}$=$\frac{1}{2}$，又∵∠PCD=∠BCP，∴△PCD∽△BCP．∴$\frac{PD}{BP}$=$\frac{1}{2}$，∴PD=$\frac{1}{2}$BP，∴AP+$\frac{1}{2}$BP=AP+PD．
请你完成余下的思考，并直接写出答案：AP+$\frac{1}{2}$BP的最小值为$\sqrt{37}$．
（2）自主探索：在“问题提出”的条件不变的情况下，$\frac{1}{3}$AP+BP的最小值为$\frac{2}{3}\sqrt{37}$．
（3）拓展延伸：已知扇形COD中，∠COD=90°，OC=6，OA=3，OB=5，点P是$\widehat{CD}$上一点，求2PA+PB的最小值．

Answer 1

分析 （1）利用勾股定理即可求出，最小值为AD=$\sqrt{37}$；
（2）连接CP，在CA上取点D，使CD=$\frac{2}{3}$，则有$\frac{CD}{CP}=\frac{CP}{CA}=\frac{1}{3}$，可证△PCD∽△ACP，得到PD=$\frac{1}{3}$AP，即：$\frac{1}{3}$AP+BP=BP+PD，从而$\frac{1}{3}$AP+BP的最小值为BD；
（3）延长OA到点E，使CE=6，连接PE、OP，可证△OAP∽△OPE，得到EP=2PA，得到2PA+PB=EP+PB，当E、P、B三点共线时，得到最小值．

解答 解：（1）如图1，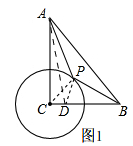

连结AD，
∵AP+$\frac{1}{2}$BP=AP+PD，要使AP+$\frac{1}{2}$BP最小，
∴AP+AD最小，当点A，P，D在同一条直线时，AP+AD最小，
即：AP+$\frac{1}{2}$BP最小值为AD，
在Rt△ACD中，CD=1，AC=6，
∴AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{37}$，
AP+$\frac{1}{2}$BP的最小值为$\sqrt{37}$，故答案为：$\sqrt{37}$；

（2）如图2，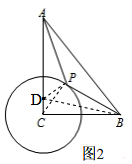

连接CP，在CA上取点D，使CD=$\frac{2}{3}$，
∴$\frac{CD}{CP}=\frac{CP}{CA}=\frac{1}{3}$，
∵∠PCD=∠ACP，
∴△PCD∽△ACP，
∴$\frac{PD}{AP}=\frac{1}{3}$，
∴PD=$\frac{1}{3}$AP，
∴$\frac{1}{3}$AP+BP=BP+PD，
∴同（1）的方法得出$\frac{1}{3}$AP+BP的最小值为BD=$\sqrt{B{C}^{2}+C{D}^{2}}$=$\frac{2}{3}\sqrt{37}$．
故答案为：$\frac{2}{3}\sqrt{37}$；

（3）如图3，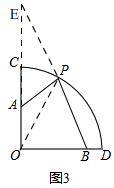

延长OA到点E，使CE=6，
∴OE=OC+CE=12，
连接PE、OP，
∵OA=3，
∴$\frac{OA}{OP}=\frac{OP}{OE}=\frac{1}{2}$，
∵∠AOP=∠AOP，
∴△OAP∽△OPE，
∴$\frac{AP}{EP}=\frac{1}{2}$，
∴EP=2PA，
∴2PA+PB=EP+PB，
∴当E、P、B三点共线时，取得最小值为：BE=$\sqrt{O{B}^{2}+O{E}^{2}}$=13．

点评 此题是一次函数综合题，主要考查了勾股定理，相似三角形的判定和性质，极值的确定，还考查了学校的阅读理解能力，解本题的关键是根据材料中的思路构造出△PCD∽△ACP和△OAP∽△OPE，也是解本题的难点．