
分析 (1)根据题意可以列出相应的不等式,从而可以求得每辆车的日租金至少应为多少元;
(2)根据题意可以得到w与x的函数关系式;
(3)由题意和(2)中的条件可以求得使游客得到实惠,当天的观光车的日租金.
解答 解:(1)由题意知,
若观光车能全部租出,则0<x≤100,
50x-1100>0,
解得x>22,
又∵x是5的倍数,
∴每辆车的日租金至少应为25元;
(2)∵每辆车的净收入为w元,
∴当0<x≤100时,w1=50x-1100;
当x>100时,w2=x(50-$\frac{x-100}{5}$)-1100=-$\frac{1}{5}$x2+70x-1100,
即w=$\left\{\begin{array}{l}{50x-1100}&{0<x≤100}\\{-\frac{1}{5}{x}^{2}+70x-1100}&{x>100}\end{array}\right.$;
(3)∵w=4420,
∴当0<x≤100时,
50x-1100=4420,
得x=110.4(舍去),
当x>100时,有:
-$\frac{1}{5}$x2+70x-1100=4420,
解得,x1=230,x2=120,
即使游客得到实惠,则当天的观光车的日租金是120元.
点评 本题考查二次函数的应用、一元二次方程的应用,解题的关键是明确题意,找出所求问题需要的条件.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.
如图,Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm,点P从点A出发,以每秒1cm的速度沿AC运动;同时点Q从点C出发,以每秒2cm的速度沿CB运动,当Q到达点B时,点P同时停止运动.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 10%+6%=x% | B. | (1+10%)(1+6%)=2(1+x%) | C. | (1+10%)(1+6%)=(1+x%)2 | D. | 10%+6%=2•x% |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
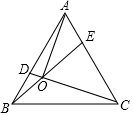 如图,点D、E分别是等边△ABC的边AB、AC上的点,满足BD=AE,连结CD、BE交于点O.已知BO=2,CO=5,则AO的长为( )
如图,点D、E分别是等边△ABC的边AB、AC上的点,满足BD=AE,连结CD、BE交于点O.已知BO=2,CO=5,则AO的长为( )| A. | 3 | B. | $\sqrt{21}$ | C. | 4 | D. | $\sqrt{19}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,AD为△ABC的中线,AB=AC,∠BAC=45°,过点C作CE⊥AB,垂足为E,CE与AD交于点F.
如图,AD为△ABC的中线,AB=AC,∠BAC=45°,过点C作CE⊥AB,垂足为E,CE与AD交于点F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 月工资/元 | 9000 | 6500 | 4000 | 3600 | 3000 | 1500 |
| 人数/人 | 1 | 1 | 4 | 3 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com