
 如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.
如图,△ABC中,∠ACB=90°,D为AB上一点,以CD为直径的⊙O交BC于点E,连接AE交CD于点P,交⊙O于点F,连接DF,∠CAE=∠ADF.分析 (1)结论:AB是⊙O切线,连接DE,CF,由∠FCD+∠CDF=90°,只要证明∠ADF=∠DCF即可解决问题.
(2)只要证明△PCF∽△PAC,得$\frac{PC}{PA}$=$\frac{PF}{PC}$,设PC=a.则PA=2a,列出方程即可解决问题.
解答 解:(1)AB是⊙O切线.
理由: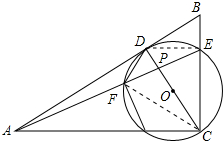 连接DE、CF.
连接DE、CF.
∵CD是直径,
∴∠DEC=∠DFC=90°,
∵∠ACB=90°,
∴∠DEC+∠ACE=180°,
∴DE∥AC,
∴∠DEA=∠EAC=∠DCF,
∵∠DFC=90°,
∴∠FCD+∠CDF=90°,
∵∠ADF=∠EAC=∠DCF,
∴∠ADF+∠CDF=90°,
∴∠ADC=90°,
∴CD⊥AD,
∴AB是⊙O切线.
(2)∵∠CPF=∠CPA,∠PCF=∠PAC,
∴△PCF∽△PAC,
∴$\frac{PC}{PA}$=$\frac{PF}{PC}$,
∴PC2=PF•PA,设PC=a.则PA=2a,
∴a2=3×2a,
∴a=6,
∴PA=2a=12,
则AF=12-3=9.
点评 本题考查切线的判定、相似三角形的判定和性质、圆的有关性质等知识,解题的关键是添加辅助线,记住直径所对的圆周角是直角,学会用方程的思想解决问题,属于中考常考题型.


 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.
如图:甲转盘被分成3个面积相等的扇形、乙转盘被分成2个面积相等的扇形.两圆心中心各有一个可以自由转动的指针,随机地转动指针(当指针指在边界线上时视为无效,重转).请回答下列问题.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
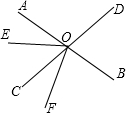 如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.
如图,直线AB、CD相交于点O.已知∠BOD=75°,OE把∠AOC分成两个角,且∠AOE:∠EOC=2:3.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
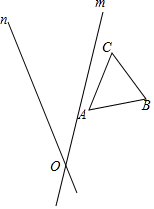 如图,直线m,n的夹角为35°,相交于点O,
如图,直线m,n的夹角为35°,相交于点O,查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com