
 如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )
如图,在⊙O中,直径CD⊥弦AB,则下列结论中正确的是( )| A. | AC=AB | B. | ∠C=$\frac{1}{2}$∠BOD | C. | ∠C=∠B | D. | ∠A=∠BOD |
分析 根据垂径定理得出$\widehat{AD}$=$\widehat{BD}$,$\widehat{AC}$=$\widehat{BC}$,根据以上结论判断即可.
解答 解:A、根据垂径定理不能推出AC=AB,故A选项错误;
B、∵直径CD⊥弦AB,
∴$\widehat{AD}$=$\widehat{BD}$,
∵$\widehat{AD}$对的圆周角是∠C,$\widehat{BD}$对的圆心角是∠BOD,
∴∠BOD=2∠C,故B选项正确;
C、不能推出∠C=∠B,故C选项错误;
D、不能推出∠A=∠BOD,故D选项错误;
故选:B
点评 本题考查了垂径定理的应用,关键是根据学生的推理能力和辨析能力来分析.


 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:选择题
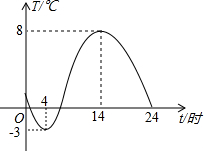 如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )
如图,是一台自动测温记录仪的图象,它反映了我市冬季某天气温T随时间t变化而变化的关系,观察图象得到下列信息,其中错误的是( )| A. | 凌晨4时气温最低为-3℃ | |
| B. | 14时气温最高为8℃ | |
| C. | 从0时至14时,气温随时间增长而上升 | |
| D. | 从14时至24时,气温随时间增长而下降 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
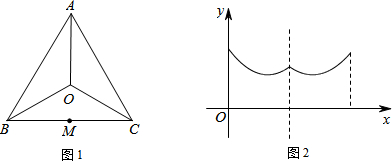
| A. | A→O→B | B. | B→A→C | C. | B→O→C | D. | C→B→O |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
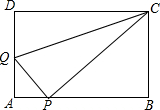 如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是8米(平面镜的厚度忽略不计).
如图是小明设计用手电来测量都匀南沙州古城墙高度的示意图,点P处放一水平的平面镜,光线从点A出发经过平面镜反射后刚好射到古城墙CD的顶端C处,已知AB⊥BD,CD⊥BD,且测得AB=1.2米,BP=1.8米,PD=12米,那么该古城墙的高度是8米(平面镜的厚度忽略不计).查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 选作题(请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.)
选作题(请从以下两个小题中任选一题作答,若多选,则按所选的第一题计分.)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com