
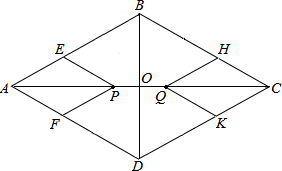
 ����ABCD�ı߳�Ϊ2����BAD=60�㣬�Խ���AC��BD�ཻ�ڵ�O������P���߶�AC�ϴӵ�A���C�˶�����P��PE��AD����AB�ڵ�E����P��PF��AB����AD�ڵ�F���ı���QHCK���ı���PEAF����ֱ��BD�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1��AP=x��
����ABCD�ı߳�Ϊ2����BAD=60�㣬�Խ���AC��BD�ཻ�ڵ�O������P���߶�AC�ϴӵ�A���C�˶�����P��PE��AD����AB�ڵ�E����P��PF��AB����AD�ڵ�F���ı���QHCK���ı���PEAF����ֱ��BD�Գƣ�������ABCD���������ı��θ�ס���ֵ����ΪS1��AP=x������ ��1���������ε����ʵó�AB=AD=2��BO=DO��AC��BD�������ABD�ǵȱ������Σ��Ƴ�BD=AB=2�����ݹ��ɶ������AO�����ɵó��𰸣�
��2���ٵ�0��x��$\sqrt{3}$ʱ������������ε���������ɵó��𰸣��ڵ�$\sqrt{3}$��x��2$\sqrt{3}$ʱ��S1���ڴ�����ABCD��ȥδ���ڸǵ�����С���Σ��������С���ε�������ɣ�
��3����$\sqrt{3}$��x��2$\sqrt{3}$ʱ�����ص����г����̣�������̵Ľ⼴�ɣ�
��� �⣺��1�����ı���ABCD�����Σ�
��AB=AD=2��BO=DO��AC��BD��
�ߡ�BAD=60�㣬
���ABD�ǵȱ������Σ�
��BD=AB=2��
��OB=OD=1��
�ɹ��ɶ����ã�AO=$\sqrt{{2}^{2}-{1}^{2}}$=$\sqrt{3}$��
��AC=2$\sqrt{3}$��
S����ABCD=$\frac{1}{2}$BD��AC=$\frac{1}{2}$��2��2$\sqrt{3}$=2$\sqrt{3}$��
�ʴ�Ϊ��2$\sqrt{3}$��2$\sqrt{3}$��
��2�����������֪�ı���PEAF�����Σ���һ������60�㣬���εĽ϶̶Խ�����߳���ȣ�
�ٵ�0��x��$\sqrt{3}$ʱ����ͼ1������EF��AP��M��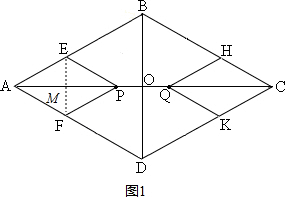
��AP=x��PE��AD��PF��AB��
��AEPF��ƽ���ı��Σ�
���ı���ABCD�����Σ�
���BAC=��DAC��
��PE��AD��
���EPA=��DAC��
���EPA=��BAC��
��AE=PE��
���ı���AEPF�����Σ�
���ı���AEPF���ı���CHQK����BD�Գƣ�
���ı���CHQKҲ�����Σ�
��EM=FM��AM=PM��AE=AF��
�ߡ�BAC=60�㣬
���AEF�ǵȱ������Σ�
��AP��EF��
�ߡ�BAC=��DAC=30�㣬AM=$\frac{1}{2}$AP=$\frac{1}{2}$x��
��EM=AM��tan30��=$\frac{\sqrt{3}}{6}$x��AE=2EM=$\frac{\sqrt{3}}{3}$x��
S����PEAF=$\frac{1}{2}$AP•EF=$\frac{1}{2}$x•$\frac{\sqrt{3}}{3}$x=$\frac{\sqrt{3}}{6}$x2��
��S1=2S����PEAF=$\frac{\sqrt{3}}{3}$x2��
�ڵ�$\sqrt{3}$��x��2$\sqrt{3}$ʱ����ͼ2��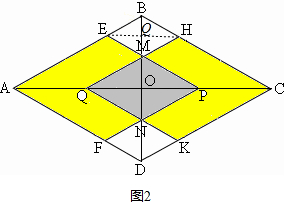
��S1���ڴ�����ABCD��ȥδ���ڸǵ�����С���Σ�
������PEAF�ı߳�AEΪ$\frac{\sqrt{3}}{3}$x��
��BE=2-$\frac{\sqrt{3}}{3}$x��
��S����BEMH=2��$\frac{\sqrt{3}}{4}$��2-$\frac{\sqrt{3}}{3}$x��2=$\frac{\sqrt{3}}{6}$x2-2x+2$\sqrt{3}$��
��S1=2$\sqrt{3}$-2S����BEMH=-$\frac{\sqrt{3}}{3}$x2+4x-2$\sqrt{3}$��
��S1=-$\frac{\sqrt{3}}{3}$x2+4x-2$\sqrt{3}$��
��S1=$\left\{\begin{array}{l}{{\frac{\sqrt{3}}{3}x}^{2}��0��x��\sqrt{3}��}\\{-\frac{\sqrt{3}}{3}{x}^{2}+4x-2\sqrt{3}��\sqrt{3}��x��2\sqrt{3}��}\end{array}\right.$��
��3�������ص���
�൱$\sqrt{3}$��x��2$\sqrt{3}$����ʱOP=x-$\sqrt{3}$��
���ص�����QMPN�ı߳�MP=MN=$\frac{2\sqrt{3}}{3}$x-2��
��S2=$\frac{1}{2}$PQ•MN=$\frac{1}{2}$��2��x-$\sqrt{3}$����$\frac{2\sqrt{3}}{3}$x-2��=$\frac{2\sqrt{3}}{3}$x2-4x+2$\sqrt{3}$��
��$\frac{2\sqrt{3}}{3}$x2-4x+2$\sqrt{3}$=$\sqrt{3}$��
��ã�x=$\sqrt{3}$��$\frac{\sqrt{6}}{2}$�������������x=$\sqrt{3}$+$\frac{\sqrt{6}}{2}$��
���� ���⿼���˹��ɶ��������ε����ʣ����ɶ������ȱ������ε����ʺ��ж�����ֱ�������ε�Ӧ�ã����ۺ�����֪ʶ����м����ǽ����Ĺؼ�����Ŀ�ۺ��ԱȽ�ǿ���Ѷ�ƫ�����˷�������˼�룮


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
| ���ӻ��ͺ� | A�� | B�� | C�� |
| ��������̨�� | 5 | 10 | 20 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2x2��x2=2x | B�� | ��-$\frac{1}{2}$a2b��3=-$\frac{1}{6}$a6b3 | C�� | 3x2+2x2=5x2 | D�� | ��x-3��2=x2-9 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ����ǵIJ���һ���Ƕ۽� | |
| B�� | ͬ�ǻ�Ƚǵ������� | |
| C�� | �����ľ�����������������߶εij��� | |
| D�� | ��ֱ��l�ϵ�һ������ֻ��һ��ֱ�ߴ�ֱ��l |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
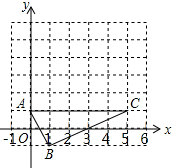 ��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ���A��B��C������ֱ�Ϊ��0��1������1��-1������5��1��
��ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC������������ڸ���ϣ���A��B��C������ֱ�Ϊ��0��1������1��-1������5��1���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͬλ����ȣ���ֱ��ƽ�� | |
| B�� | ��ֱ��ƽ�У��ڴ������ | |
| C�� | ��ֱ�߱�������ֱ�����أ��ڴ������ | |
| D�� | ͬ���ڽǻ�������ֱ��ƽ�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
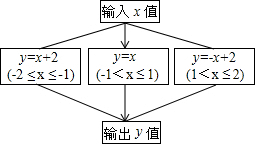
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com