
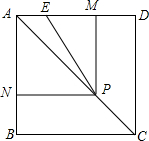
 如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.
如图,已知正方形ABCD的边长为1,P是对角线AC上任意一点,E为AD上的点,且∠EPB=90°,PM⊥AD,PN⊥AB.分析 (1)由正方形的性质得出∠BAD=90°,AC平分∠BAD,证出PM=PN,∠PMA=∠PNA=90°,即可得出结论;
(2)作PF⊥BC于F,由正方形的性质得出∠ABC=90°,AB=BC=1,∠PCF=45°,由勾股定理求出AC,证出△PCF是等腰直角三角形,得出AP=AC-PC=$\sqrt{2}$-x,BN=PF=$\frac{\sqrt{2}}{2}$x,由正方形的性质得出PM=PN,证出∠MPE=∠NPB,由ASA证明△EPM≌△BPN,得出EM=BN=$\frac{\sqrt{2}}{2}$x,证出△APM是等腰直角三角形,得出AP=$\sqrt{2}$AM=$\sqrt{2}$(AE+EM),即可得出结果.
解答 (1)证明:∵四边形ABCD是正方形,
∴∠BAD=90°,AC平分∠BAD,
∵PM⊥AD,PN⊥AB,
∴PM=PN,∠PMA=∠PNA=90°,
∴四边形PMAN是矩形,
∴四边形PMAN是正方形;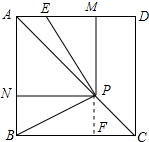
(2)解:作PF⊥BC于F,如图所示:
∵四边形ABCD是正方形,
∴∠ABC=90°,AB=BC=1,∠PCF=45°,
∴AC=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,△PCF是等腰直角三角形,
∴AP=AC-PC=$\sqrt{2}$-x,BN=PF=$\frac{\sqrt{2}}{2}$x,
∵四边形PMAN是正方形,
∴PM=PN,∠MPN=90°,
∵∠EPB=90°,
∴∠MPE=∠NPB,
在△EPM和△BPN中,
$\left\{\begin{array}{l}{∠PMA=∠PNB=90°}&{\;}\\{PM=PN}&{\;}\\{∠MPE=∠NPB}&{\;}\end{array}\right.$,
∴△EPM≌△BPN(ASA),
∴EM=BN=$\frac{\sqrt{2}}{2}$x,
∵∠PAM=45°,∠PMA=90°,
∴△APM是等腰直角三角形,
∴AP=$\sqrt{2}$AM=$\sqrt{2}$(AE+EM),
即$\sqrt{2}$-x=$\sqrt{2}$(y+$\frac{\sqrt{2}}{2}$x),
解得:y=1-$\sqrt{2}$x,x的取值范围为0≤x≤$\frac{\sqrt{2}}{2}$.
点评 本题考查了正方形的性质与判定、勾股定理、等腰直角三角形的判定与性质、全等三角形的判定与性质;熟练掌握正方形的性质,证明三角形全等是解决问题(2)的关键.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:初中数学 来源: 题型:选择题
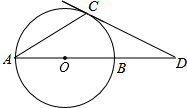 如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )
如图,AB是⊙O的直径,点C是⊙O上一点,过点C的切线与AB的延长线交于点D,连接AC、CO,若∠A=35°,则∠ADC的度数为( )| A. | 20° | B. | 30° | C. | 35° | D. | 55° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:
在平面直角坐标系xOy中,对于点P(a,b)和点Q(a,b′),给出如下定义:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 售价(元/件) | 100 | 110 | 120 | 130 | … |
| 月销量(件) | 200 | 180 | 160 | 140 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
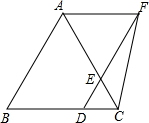 已知△ABC为边长为6的等边三角形,D、E分别在边BC、AC上,且CD=CE=x,连接
已知△ABC为边长为6的等边三角形,D、E分别在边BC、AC上,且CD=CE=x,连接查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com