
【题目】在△ABC中,∠BAC=90°,AB=AC,AD⊥BC于点D.过射线AD上一点M作BM的垂线,交直线AC于点N.
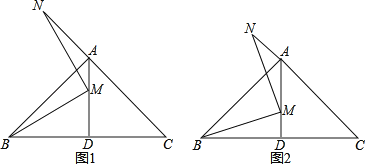
(1)如图1,点M在AD上,若∠N=15°,BC=2![]() ,则线段AM的长为 ;
,则线段AM的长为 ;
(2)如图2,点M在AD上,求证:BM=NM;
(3)若点M在AD的延长线上,则AB,AM,AN之间有何数量关系?直接写出你的结论,不证明.
【答案】(1)![]() ﹣1;(2)见解析;(3)
﹣1;(2)见解析;(3)![]() AM.
AM.
【解析】
(1)证得∠ABM=15°,则∠MBD=30°,求出DM=1,则AM可求出;
(2)过点M作AD的垂线交AB于点E,根据ASA可证明△BEM≌△NAM,得出BM=NM;
(3)过点M作AD的垂线交AB于点E,同(2)可得△AEM为等腰直角三角形,证明△BEM≌△NAM,BE=AN,则问题可解;
解:(1)∵∠N=15°,∠BMN=∠BAN=90°,
∴∠ABM=15°,
∵AB=AC,∠BAC=90°,AD⊥BC,
∴∠ABC=∠C=45°,BD=CD,
∴∠MBD=∠ABD﹣∠ABM=45°﹣15°=30°.
∴DM=![]() .
.
∴![]() ﹣1.
﹣1.
故答案为:![]() ﹣1;
﹣1;
(2)过点M作AD的垂线交AB于点E,
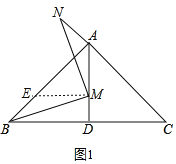
∵∠BAC=90°,AB=AC,AD⊥BC,
∴∠NAB=90°,∠BAD=45°,
∴∠AEM=90°﹣45°=45°∠BAD,
∴EM=AM,∠BEM=135°,
∵∠NAB=90°,∠BAD=45°,
∴∠NAD=135°,
∴∠BEM=∠NAD,
∵EM⊥AD,
∴∠AMN+∠EMN=90°,
∵MN⊥BM,
∴∠BME+∠EMN=90°,
∴∠BME=∠AMN,
在△BEM和△NAM中,
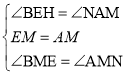 ,
,
∴△BEM≌△NAM(ASA),
∴BM=NM;
(3)数量关系是:AB+AN=![]() AM.
AM.
证明:过点M作AD的垂线交AB于点E,
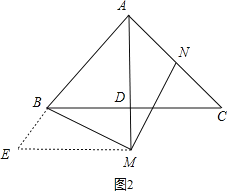
同(2)可得△AEM为等腰直角三角形,
∴∠E=45°,AM=EM,
∵∠AME=∠BMN=90°,
∴∠BME=∠AMN,
在△BEM和△NAM中,
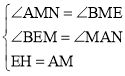 ,
,
∴△BEM≌△NAM(AAS),
∴BE=AN,
∴![]() AM.
AM.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系内,边长为 4 的等边△ABC 的顶点 B 与原点重合,将△ABC 绕顶点 C 顺时针旋转 60°得到△ACA1,将四边形 ABCA1看作一个基本图形,将此基本图形不断复制并平移,请回答:
(1)求点 A的坐标;点 A1的坐标.
(2)求A2018的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校计划购买若干台电脑,现从两家商场了解到同一型号电脑每台报价均为4000元,并且多买都有一定的优惠.甲商场的优惠条件是:第一台按原价收费,其余每台优惠25%;乙商场的优惠条件是:每台优惠20%.
(1)设该学校所买的电脑台数是x台,选择甲商场时,所需费用为![]() 元,选择乙商场时,所需费用为
元,选择乙商场时,所需费用为![]() 元,请分别写出
元,请分别写出![]() ,
, ![]() 与x之间的关系式;
与x之间的关系式;
(2)该学校如何根据所买电脑的台数选择到哪间商场购买,所需费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】满足下列条件的△ABC不是直角三角形的是( )
A.AC=1,BC=![]() ,AB=2B.AC:BC:AB=3:4:5
,AB=2B.AC:BC:AB=3:4:5
C.∠A:∠B:∠C=1:2:3D.∠A:∠B:∠C=3:4:5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某汽车交易市场为了解二手轿车的交易情况,将本市场去年成交的二手轿车的全部数据,以二手轿车交易前的使用时间为标准分为A、B、C、D、E五类,并根据这些数据由甲,乙两人分别绘制了下面的两幅统计图(图都不完整).

请根据以上信息,解答下列问题:
(1)该汽车交易市场去年共交易二手轿车 辆.
(2)把这幅条形统计图补充完整.(画图后请标注相应的数据)
(3)在扇形统计图中,D类二手轿车交易辆数所对应扇形的圆心角为 度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分9分)深圳大运会期间,某宾馆有若干间住房,住宿记录提供了如下信息:①7月20日全部住满,一天住宿费收入为3600元;②7月21日有10间房空着,一天住宿费收入为2800元;③该宾馆每间房每天收费标准相同。
【1】(1)求该宾馆共有多少间住房,每间住房每天收费多少元?
【2】(2)通过市场调查发现,每个住房每天的定价每增加10元,就会有一个房间空闲;己知该宾馆空闲房间每天每间费用10元,有游客居住房间每天每间再增加20元的其他费用,问房价定为多少元时,该宾馆一天的利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
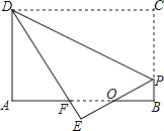
【题目】如图,矩形纸片ABCD,AB=5,BC=3,点P在BC边上,将△CDP沿DP折叠,点C落在点E处,PE,DE分别交AB于点O,F,且OP=OF,则AF的值为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com