
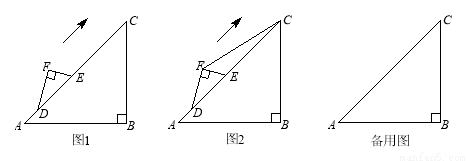
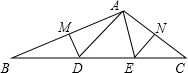
图1是李晨在一次课外活动中所做的问题研究:他用硬纸片做了两个三角形,分别为△ABC和△DEF,其中∠B=90°,∠A=45°,BC=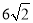 ,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
,∠F=90°,∠EDF=30°, EF=2.将△DEF的斜边DE与△ABC的斜边AC重合在一起,并将△DEF沿AC方向移动.在移动过程中,D、E两点始终在AC边上(移动开始时点D与点A重合).
(1)请回答李晨的问题:若CD=10,则AD= ;
(2)如图2,李晨同学连接FC,编制了如下问题,请你回答:
①∠FCD的最大度数为 ;
②当FC∥AB时,AD= ;
③当以线段AD、FC、BC的长度为三边长的三角形是直角三角形,且FC为斜边时,AD= ;
④△FCD的面积s的取值范围是 .
(1)2;(2)① 60°;② 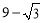 ;③
;③ 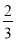 ;④
;④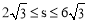 .
.
【解析】
试题分析:(1)根据等腰直角三角形的性质,求出AC的长,即可得到AD的长.
(2)①当点E与点C重合时,∠FCD的角度最大,据此求解即可.
②过点F作FH⊥AC于点H,应用等腰直角三角形的判定和性质,含30度角直角三角形的性质求解即可.
③过点F作FH⊥AC于点H,AD=x,应用含30度角直角三角形的性质把FC用x来表示,根据勾股定理列式求解.
④设AD=x,把△FCD的面积s表示为x的函数,根据x的取值范围来确定s的取值范围.
试题解析:(1)∵∠B=90°,∠A=45°,BC= ,∴AC=12.
,∴AC=12.
∵CD=10,∴AD=2.
(2)①∵∠F=90°,∠EDF=30°,∴∠DEF=60°.
∵当点E与点C重合时,∠FCD的角度最大,∴ ∠FCD的最大度数=∠DEF=60°.
② 如图,过点F作FH⊥AC于点H,
∵∠EDF=30°, EF=2,∴DF= . ∴DH=3,FH=
. ∴DH=3,FH=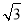 .
.
∵FC∥AB,∠A=45°,∴∠FCH=45°. ∴HC=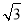 . ∴DC=DH+HC=
. ∴DC=DH+HC=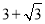 .
.
∵AC=12,∴AD=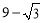 .
.
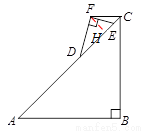
③如图,过点F作FH⊥AC于点H,设AD=x,
由②知DH=3,FH=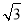 ,则HC=
,则HC=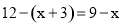 .
.
在Rt△CFH中,根据勾股定理,得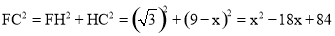 .
.
∵以线段AD、FC、BC的长度为三边长的三角形是直角三角形,且FC为斜边,
∴ ,即
,即 ,解得
,解得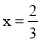 .
.

④设AD=x,易知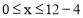 ,即
,即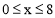 .
.
而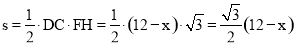 ,
,
当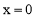 时,
时,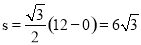 ;当
;当 时,
时,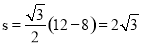 .
.
∴△FCD的面积s的取值范围是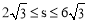 .
.
考点:1.面动平移问题;2. 等腰直角三角形的判定和性质;3.平行的性质;4. 含30度角直角三角形的性质;5.勾股定理;6.由实际问题列函数关系式;7.求函数值.


 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:初中数学 来源:2013-2014学年北京市昌平区中考一模数学试卷(解析版) 题型:解答题
列方程解应用题:
王亮的父母每天坚持走步锻炼. 今天王亮的妈妈以每小时3千米的速度走了10分钟后,王亮的爸爸刚好看完球赛,马上沿着妈妈所走的路线以每小时4千米的速度追赶,求爸爸追上妈妈时所走的路程.
查看答案和解析>>
科目:初中数学 来源:2013-2014学年北京市大兴区中考一模数学试卷(解析版) 题型:解答题
列方程(组)解应用题:
某工厂现在平均每天比原计划平均每天多生产50台机器,现在生产600台机器所需的时间与原计划生产400台机器所需的时间相同,现在平均每天生产多少台机器?
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
| A.24和12 | B.16和22 | C.20和16 | D.22和16 |
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题

查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com