
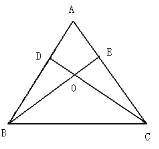
【题目】已知:如图,锐角△ABC的两条高BE、CD相交于点O,且OB=OC,
(1)求证:△ABC是等腰三角形;
(2)判断点O是否在∠BAC的角平分线上,并说明理由。
【答案】(1)、证明过程见解析;(2)、理由见解析
【解析】
试题分析:(1)、根据等腰三角形的性质以及高线得出△BDC和△CEB全等,从而得出∠DBC=∠ECB,得到等腰三角形;(2)、连接AO,根据△BDC和△CEB全等得到DC=EB,然后根据OB=OC得出OD=OE,结合∠BDC=∠CEB=90°和AO为公共边得出△ADO和△AEO全等从而得到答案.
试题解析:(1)、∵OB=OC ∴∠OBC=∠OCB ∵BE、CD是两条高 ∴∠BDC=∠CEB=90°
又∵BC=CB ∴△BDC≌△CEB(AAS) ∴∠DBC=∠ECB ∴AB=AC ∴△ABC是等腰三角形。
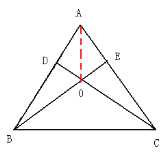
(2)、点O是在∠BAC的角平分线上。连结AO. ∵ △BDC≌△CEB ∴DC=EB,
∵OB=OC ∴ OD=OE 又∵∠BDC=∠CEB=90° AO=AO ∴△ADO≌△AEO(HL)
∴∠DAO=∠EAO ∴点O是在∠BAC的角平分线上。


科目:初中数学 来源: 题型:
【题目】关于零的说法,下列正确的选项是( )
A. 零是最小的整数 B. 零的相反数是零
C. 零与任何数相加得零 D. 两数相乘得零,则这两个数都为零
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形![]() 是正方形,
是正方形,![]() 与
与![]() 相交于点
相交于点![]() ,点
,点![]() 、
、![]() 是直线
是直线![]() 上两动点,且
上两动点,且![]() ,
,![]() 所在直线与对角线
所在直线与对角线![]() 所在直线交于点
所在直线交于点![]() ,连接
,连接![]() ,直线
,直线![]() 交
交![]() 于点
于点![]() .
.
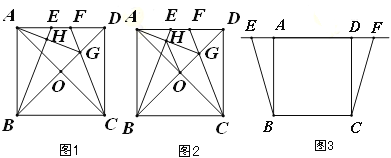
(1)如图1,当点![]() 、
、![]() 在线段
在线段![]() 上时,
上时,
①求证:![]() ;
;
②猜想![]() 与
与![]() 的位置关系,并加以证明;
的位置关系,并加以证明;
(2)如图2,在(1)条件下,连接![]() ,试说明
,试说明![]() 平分
平分![]() ;
;
(3)当点![]() 、
、![]() 运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出
运动到如图3所示的位置时,其它条件不变,请将图形补充完整,并直接写出![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
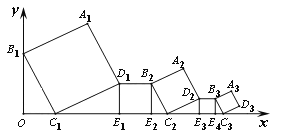
【题目】如图,在平面直角坐标系中放置了5个正方形,点B1(0,2)在y轴上,点C1,E1,E2,C2,E3,E4,C3在x轴上,C1的坐标是(1, 0),B1C1∥B2C2∥B3C3.点A3到x轴的距离是.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com