Question

解下列方程组
（1）
（2）
（3）
（4）．

Answer 1

解：（1），
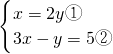
将①代入②得：6y-y=5，
解得：y=1，
将y=1代入①得：x=2，
则方程组的解为；
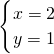
（2），
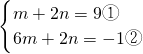
②-①得：5m=-10，
解得：m=-2，
将m=-2代入①得：-2+2n=9，
解得：n=，
则方程组的解为；
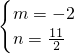
（3），
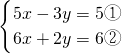
①×2+②×3得：28x=28，
解得：x=1，
将x=1代入①得：5-3y=5，
解得：y=0，
则方程组的解为；
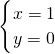
（4）方程组整理得：，
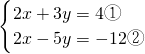
①-②得：8y=16，
解得：y=2，
将y=2代入①得：2x=-2，
解得：x=-1，
则方程组的解为．
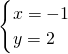
分析：（1）将第一个方程代入第二个方程中消去x求出y的值，进而求出x的值，即可得到方程组的解；
（2）两方程相减消去n求出m的值，进而求出n的值，即可得到方程组的解；
（3）第一个方程乘以2减去第二个方程乘以3消去y求出x的值，进而求出y的值，即可得到方程组的解；
（4）方程组整理后，利用加减消元法求出解即可．
点评：此题考查了 解二元一次方程组，利用了消元的思想，消元的方法有：加减消元法与代入消元法．
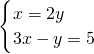
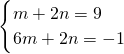
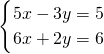
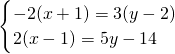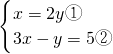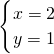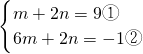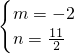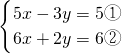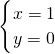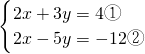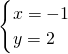