练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】不等式组 的解集在数轴上表示正确的是（ ）
    A.
    B.
    C.
    D.

    【答案】B
    【解析】解：（1）移项、合并同类项得，x＞﹣2，（2）去括号得，﹣x+4≥1，移项、合并得，﹣x≥﹣3，化系数为1得，x≤3，

    故原不等式组的解集为：﹣2＜x≤3．

    在数轴上表示为：

    所以答案是：B．

    【考点精析】掌握不等式的解集在数轴上的表示和一元一次不等式组的解法是解答本题的根本，需要知道不等式的解集可以在数轴上表示，分三步进行：①画数轴②定界点③定方向．规律：用数轴表示不等式的解集，应记住下面的规律：大于向右画，小于向左画，等于用实心圆点，不等于用空心圆圈；解法：①分别求出这个不等式组中各个不等式的解集；②利用数轴表示出各个不等式的解集；③找出公共部分；④用不等式表示出这个不等式组的解集．如果这些不等式的解集的没有公共部分，则这个不等式组无解 ( 此时也称这个不等式组的解集为空集 )．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图一，∠ACB=90°，点D在AC上，DE⊥AB垂足为E，交BC的延长线于F，DE=EB，EG=EB，
    （1）求证：AG=DF；
    （2）过点G作GH⊥AD，垂足为H，与DE的延长线交于点M，如图二，找出图中与AB相等的线段，并证明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于数对（a，b）、（c，d），定义：当且仅当a=c且b=d时，（a，b）=（c，d）；并定义其运算如下： （a，b）※（c，d）=（ac﹣bd，ad+bc），如（1，2）※（3，4）=（1×3﹣2×4，1×4+2×3）=（﹣5，10）．若（x，y）※（1，﹣1）=（1，3），则xy的值是（ ）
    A.﹣1
    B.0
    C.1
    D.2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

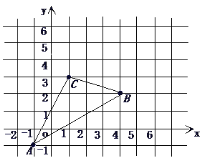
    【题目】△ABC在直角坐标系中的位置如图所示，

    （1）请你写出△ABC各点的坐标，

    （2）求出S△ABC的面积，

    （3）若把△ABC向上平移3个单位，再向右平移2个单位得△A′B′C′，在图中画出△A′B′C′，并写出A′、B′、C′的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在一次知识竞赛中，甲、乙两人进入了“必答题”环节．规则是：两人轮流答题，每人都要回答20个题，每个题回答正确得a分，回答错误或放弃回答扣b分．当甲、乙两人恰好都答完12个题时，甲答对了8个题，得分为64分；乙答对了9个题，得分为78分．

    （1）求a和b的值；

    （2）规定此环节得分不低于120分能晋级，甲在剩下的比赛中至少还要答对多少个题才能顺利晋级？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在某次人才交流会上，应聘人数和招聘人数分别居前5位的行业列表如下：

    如果用同一行业应聘人数与招聘人数比值的大小来衡量该行业的就业情况，那么根据表中数据，对上述行业的就业情况判断正确的是(　　)

    A. 计算机行业好于其它行业 B. 贸易行业好于化工行业

    C. 机械行业好于营销行业 D. 建筑行业好于物流行业

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，E是等边三角形ABC的边AB所在直线上一点，D是边BC所在直线上一点，且D与C不重合，若EC＝ED．则称D为点C关于等边三角形ABC的反称点，点E称为反称中心．

    在平面直角坐标系xOy中，

    （1）已知等边三角形AOC的顶点C的坐标为（2，0），点A在第一象限内，反称中心E在直线AO上，反称点D在直线OC上．

    ①如图2，若E为边AO的中点，在图中作出点C关于等边三角形AOC的反称点D，并直接写出点D的坐标：　 　；

    ②若AE＝2，求点C关于等边三角形AOC的反称点D的坐标；

    （2）若等边三角形ABC的顶点为B（n，0），C（n+1，0），反称中心E在直线AB上，反称点D在直线BC上，且2≤AE＜3．请直接写出点C关于等边三角形ABC的反称点D的横坐标t的取值范围：　 　（用含n的代数式表示）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，锐角△ABC中，D，E分别是AB，AC边上的点，△ADC≌△ADC'，△AEB≌△AEB'，且C'D∥EB'∥BC，记BE，CD交于点F，若∠BAC＝x°，则∠BFC的大小是_____°．（用含x的式子表示）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某学校后勤人员到一家文具店给九年级的同学购买考试用文具包，文具店规定一次购买400个以上，可享受8折优惠.若给九年级学生每人购买一个，不能享受8折优惠，需付款1936元；若多买88个，就可享受8折优惠，同样只需付款1936元.请问该学校九年级学生有多少人？

    查看答案和解析>>

    同步练习册答案