
【题目】如图,锐角△ABC中,D,E分别是AB,AC边上的点,△ADC≌△ADC',△AEB≌△AEB',且C'D∥EB'∥BC,记BE,CD交于点F,若∠BAC=x°,则∠BFC的大小是_____°.(用含x的式子表示)

【答案】![]()
【解析】
延长C′D交AC于M,如图,根据全等的性质得∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,再利用三角形外角性质得∠C′MC=∠C′+∠C′AM=∠C′+2x,接着利用C′D∥B′E得到∠AEB=∠C′MC,而根据三角形内角和得到∠AEB′=180°-∠B′-x,则∠C′+2x=180°-∠B′-x,所以∠C′+∠B′=180°-3x,利用三角形外角性质和等角代换得到∠BFC=∠C=x+∠C′+∠B′,所以∠BFC=180°-2x.
延长C′D交AC于M,如图,

∵△ADC≌△ADC′,△AEB≌△AEB′,∴∠C′=∠ACD,∠C′AD=∠CAD=∠B′AE=x,
∴∠C′MC=∠C′+∠C′AM=∠C′+2x,
∵C′D∥B′E,
∴∠AEB=∠C′MC,
∵∠AEB′=180°∠B′∠B′AE=180°∠B′x,
∴∠C′+2x=180°∠B′x,
∴∠C′+∠B′=180°3x,
∵∠BFC=∠BDF+∠DBF=∠DAC+∠B′=x+∠ACD+∠B′=x+∠C′+∠B′
=x+180°3x=180°2x.
故答案为:![]()


科目:初中数学 来源: 题型:
【题目】如图,一个几何体的主视图和左视图都是底边长为6,高为4的等腰三角形,俯视图是一个圆,那么这个几何体的侧面积是( ) 
A.12π
B.24π
C.![]() π
π
D.15π
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,点![]() ,
,![]() ,点
,点![]() 在第三象限,已知
在第三象限,已知![]() ,且
,且![]() .
.
(1)求点![]() 的坐标;
的坐标;
图1
(2)如图2,![]() 为线段
为线段![]() 上一动点(端点除外),
上一动点(端点除外),![]() 是
是![]() 轴负半轴的一点,连接
轴负半轴的一点,连接![]() 、
、![]() ,射线
,射线![]() 与
与![]() 的角平分线交于
的角平分线交于![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
图2
(3)在第(2)问的基础上,如图3,点![]() 与点
与点![]() 关于
关于![]() 轴对称,
轴对称,![]() 是射线
是射线![]() 上一个动点,连接
上一个动点,连接![]() ,
,![]() 平分
平分![]() ,
,![]() 平分
平分![]() ,射线
,射线![]() .试问
.试问![]() 的度数是否发生改变?若不变,请求其度数:若改变,请指出其变化范围.
的度数是否发生改变?若不变,请求其度数:若改变,请指出其变化范围.
图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为x=﹣1,与x轴的一个交点在(﹣3,0)和(﹣2,0)之间,其部分图象如图所示,则下列结论: ⑴b2﹣4ac>0;
⑵2a=b;
⑶点(﹣ ![]() ,y1)、(﹣
,y1)、(﹣ ![]() ,y2)、(
,y2)、( ![]() ,y3)是该抛物线上的点,则y1<y2<y3;
,y3)是该抛物线上的点,则y1<y2<y3;
⑷3b+2c<0;
⑸t(at+b)≤a﹣b(t为任意实数).
其中正确结论的个数是( )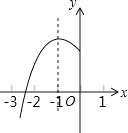
A.2
B.3
C.4
D.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在我国沿海有一艘不明国籍的轮船进入我国海域,我海军甲、乙两艘巡逻艇立即从相距13nmile的A,B两个基地前去拦截,六分钟后同时到达C地将其拦截.已知甲巡逻艇每小时航行120nmile,乙巡逻艇每小时航行50nmile,航向为北偏西40°,求甲巡逻艇的航向.
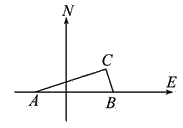
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).

A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com