【题目】让我们轻松一下，做一个数字游戏．第一步：取一个自然数
，计算
得
；第二步：算出的各位数字之和得
，计算
得
；第三步：算出的各位数字之和得
，计算
得
；
依此类推，则
的值为
A.26B.65C.122D.123
科目：初中数学 来源： 题型：
【题目】铁路货运调度站有A、B两个信号灯，在灯这旁停靠着甲、乙、丙三列火车．它们中最长的车长与居中车长之差等于居中车长与最短车长之差，其中乙车的车长居中，最开始的时候，甲、丙两车车尾对齐，且车尾正好位于A信号灯处，而车头则冲着B信号灯的方向，乙车的车尾则位于B信号灯处，车头则冲着A的方向，现在，三列火车同时出发向前行驶，3秒之后三列火车的车头恰好相遇，再过9秒，甲车恰好超过丙车，而丙车也正好完全和乙车错开，请问：甲乙两车从车头相遇直到完全错开一共用了_____秒钟．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在平面直角坐标系xOy中，当图形W上的点P的横坐标和纵坐标相等时，则称点P为图形W的“梦之点”.
（1）已知⊙O的半径为1.
①在点E（1,1），F（
,－
）,M(－2，－2)中，⊙O的“梦之点”为 ；
②若点P位于⊙O内部，且为双曲线
（k≠0）的“梦之点”，求k的取值范围.
（2）已知点C的坐标为（1，t），⊙C的半径为
，若在⊙C上存在“梦之点”P，直接写出t的取值范围.
（3）若二次函数
的图象上存在两个“梦之点”
，
,且
，求二次函数图象的顶点坐标.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】先化简，再求值：
（1）﹣3x2+3x+1+2x2﹣2x，其中x=﹣1．
（2）（a2﹣ab﹣7）﹣（﹣4a2+2ab+7）， 其中a=2，b=
．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知△ABC是等腰直角三角形，∠ACB＝90°.
(1)如图，点M在斜边AB上，且AC＝
，MA＝
，则线段MB＝___________，MC=__________；
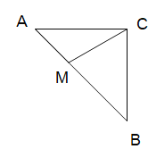
(2)如图，点M在
ABC外，MA＝2，MC＝5，∠AMC＝45°，求MB；
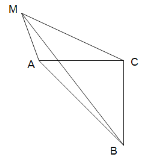
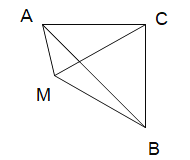
(3)如图，点M在ABC外，MA＝3，MB＝
，MC＝6，求AC.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】矩形纸片ABCD中，已知AD=8，AB=6，E是边BC上的点，以AE为折痕折叠纸片，使点B落在点F处，连接FC，当△EFC为直角三角形时，BE的长为 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
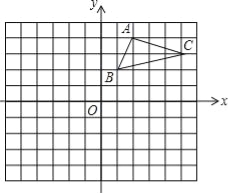
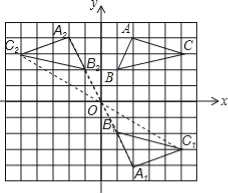
【题目】如图，在平面直角坐标系中，△ABC的三个顶点都在格点上，点A的坐标为（2，4），请解答下列问题：
（1）画出△ABC关于x轴对称的△A1B1C1，并写出点A1的坐标．
（2）画出△A1B1C1绕原点O旋转180°后得到的△A2B2C2，并写出点A2的坐标．
【答案】（1）作图见解析；点A1的坐标（2，﹣4）；（2）作图见解析；点A2的坐标（﹣2，4）．
【解析】
试题分析：（1）分别找出A、B、C三点关于x轴的对称点，再顺次连接，然后根据图形写出A点坐标；
（2）将△A1B1C1中的各点A1、B1、C1绕原点O旋转180°后，得到相应的对应点A2、B2、C2，连接各对应点即得△A2B2C2．
试题解析：（1）如图所示：点A1的坐标（2，﹣4）；
（2）如图所示，点A2的坐标（﹣2，4）．
考点：1.作图-旋转变换；2.作图-轴对称变换．
【题型】解答题
【结束】
18
【题目】观察下面的点阵图和相应的等式，探究其中的规律：
（1）认真观察，并在④后面的横线上写出相应的等式．
①1=1 ②1+2=
=3 ③1+2+3=
=6 ④ …
（2）结合（1）观察下列点阵图，并在⑤后面的横线上写出相应的等式．
1=12②1+3=22③3+6=32④6+10=42⑤ …
（3）通过猜想，写出（2）中与第n个点阵相对应的等式 ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】将一张长方形的纸对折，如图所示可得到一条折痕（图中虚线），继续对折，对折时每次折痕与上次的折痕保持平行，连续对折三次后，可以得7条折痕，那么对折四次可以得到 条折痕，如果对折
次，可以得到 条折痕．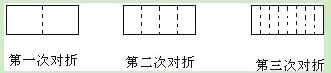
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，小岛在港口P的北偏西60°方向，距港口56海里的A处，货船从港口P出发，沿北偏东45°方向匀速驶离港口P，4小时后货船在小岛的正东方向。求货船的航行速度。（精确到0.1海里/时，参考数据：
≈1.41，
≈1.73）
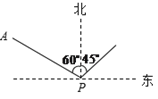
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
