
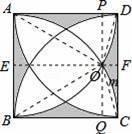
如图,正方形ABCD的边长为2,四条弧分别以相应顶点为圆心,正方形ABCD的边长为半径.求阴影部分的面积 .


16﹣4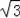
 ﹣
﹣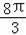
 .
.
【考点】扇形面积的计算;正方形的性质.
【专题】几何图形问题.
【分析】如解答图,作辅助线,利用图形的对称性求解.解题要点是求出弓形OmC的面积.
【解答】解:如图,设点O为弧的一个交点.
连接OA、OB,则△OAB为等边三角形,∴∠OBC=30°.
过点O作EF⊥CD,分别交AB、CD于点E、F,则OE为等边△OAB的高,
∴OE=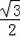
 AB=
AB=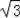
 ,∴OF=2﹣
,∴OF=2﹣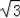
 .
.
过点O作PQ⊥BC,分别交AD、BC于点P、Q,则OQ=1.
S弓形OmC=S扇形OBC﹣S△OBC=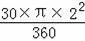
 ﹣
﹣
 ×2×1=
×2×1=
 ﹣1.
﹣1.
∴S阴影=4(S△OCD﹣2S弓形OmC)=4[
 ×2×(2﹣
×2×(2﹣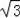
 )﹣2(
)﹣2(
 ﹣1)]=16﹣4
﹣1)]=16﹣4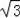
 ﹣
﹣
 .
.
故答案为:16﹣4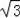
 ﹣
﹣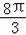
 .
.

【点评】本题考查了扇形的面积公式和正方形性质的+应用,主要考查学生的计算能力,题目比较好,难度不大.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
如图,小明用铅笔可以支起一张质地均匀的三角形卡片,则他支起的这个点应是三角形的( )
A.三边高的交点 B.三条角平分线的交点
C.三边垂直平分线的交点 D.三边中线的交点

查看答案和解析>>
科目:初中数学 来源: 题型:
某班组织活动,班委会准备用15元钱全部用来购买笔记本和中性笔两种奖品.已知笔记本2元/本,中性笔1元/支,且每种奖品至少买一件.
(1)有多少种购买方案?请列举所有可能的结果;
(2)从上述方案中任选一种方案购买,求买到的中性笔数量多于笔记本数量的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
一个不透明的口袋中装有4个分别标有数字﹣1,﹣2,3,4的小球,它们的形状、大小完全相同.小红先从口袋中随机摸出一个小球记下数字为x;小颖在剩下的3个小球中随机摸出一个小球记下数字为y.
(1)小红摸出标有数字3的小球的概率是 ;
(2)请用列表法或画树状图的方法表示出由x,y确定的点P(x,y)所有可能的结果;
(3)若规定:点P(x,y)在第一象限或第三象限小红获胜;点P(x,y)在第二象限或第四象限则小颖获胜.请分别求出两人获胜的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
在初三基础测试中,我学校的小明的6科成绩分别为语文118分,英语117分,数学117分,物理83分,化学80分,政治83分,则他的成绩的众数为 分.
查看答案和解析>>
科目:初中数学 来源: 题型:
2012年5月8日,“最美教师”张丽莉为救学生身负重伤,张老师舍己救人的事迹受到全国人民的极大关注,在住院期间,共有695万人以不同方式向她表示问候和祝福,将695万人用科学记数法表示为 人.(结果精确到十万位)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com