
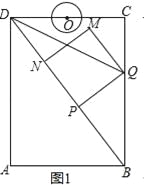
ЁОЬтФПЁПШчЭМЃЌдкОиаЮABCDжаЃЌAB=6cmЃЌAD=8cmЃЌЕуPДгЕуBГіЗЂЃЌбиЖдНЧЯпBDЯђЕуDдШЫйдЫЖЏЃЌЫйЖШЮЊ4cm/sЃЌЙ§ЕуPзїPQЁЭBDНЛBCгкЕуQЃЌвдPQЮЊвЛБпзїе§ЗНаЮPQMNЃЌЪЙЕУЕуNТфдкЩфЯпPDЩЯЃЌЕуOДгЕуDГіЗЂЃЌбиDCЯђЕуCдШЫйдЫЖЏЃЌЫйЖШЮЊ3cm/sЃЌвдOЮЊдВаФЃЌ0.8cmЮЊАыОЖзїЁбOЃЌЕуPгыЕуOЭЌЪБГіЗЂЃЌЩшЫќУЧЕФдЫЖЏЪБМфЮЊtЃЈЕЅ ЮЛЃКsЃЉЃЈ0ЃМtЃМ![]() ЃЉЁЃ
ЃЉЁЃ
ЃЈ1ЃЉШчЭМ1ЃЌСЌНгDQЦНЗжЁЯBDCЪБЃЌtЕФжЕЮЊЁЁЁЁЁЁЁЁЁЁЁЁЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌСЌНгCMЃЌШєЁїCMQЪЧвдCQЮЊЕзЕФЕШбќШ§НЧаЮЃЌЧѓtЕФжЕЃЛ
ЃЈ3ЃЉЧыФуМЬајНјааЬНОПЃЌВЂНтД№ЯТСаЮЪЬтЃК
ЂйжЄУїЃКдкдЫЖЏЙ§ГЬжаЃЌЕуOЪМжедкQMЫљдкжБЯпЕФзѓВрЃЛ
ЂкШчЭМ3ЃЌдкдЫЖЏЙ§ГЬжаЃЌЕБQMгыЁбOЯрЧаЪБЃЌЧѓtЕФжЕЃЛВЂХаЖЯДЫЪБPMгыЁбOЪЧЗёвВЯрЧаЃПЫЕУїРэгЩЃЎ

ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉ
ЃЛЃЈ2ЃЉ![]() ЃЛЃЈ3ЃЉЂйжЄУїМћНтЮіЃЌЂкt=
ЃЛЃЈ3ЃЉЂйжЄУїМћНтЮіЃЌЂкt=![]() ЃЌPMгыЁбOВЛЯрЧа.
ЃЌPMгыЁбOВЛЯрЧа.
ЁОНтЮіЁПЪдЬтЗжЮіЃКБОЬтПМВщдВзлКЯЬтЁЂе§ЗНаЮЕФаджЪЁЂЯрЫЦШ§НЧаЮЕФХаЖЈКЭаджЪЁЂЧаЯпЕФХаЖЈКЭаджЪЁЂЙДЙЩЖЈРэЁЂНЧЦНЗжЯпЕФаджЪЕШжЊЪЖЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪЙЙНЈЗНГЬЃЌзюКѓвЛИіЮЪЬтРћгУЗДжЄЗЈжЄУїНтЬтЃЎ
ЃЈ1ЃЉЯШРћгУЁїPBQЁзЁїCBDЧѓГіPQЁЂBQЃЌдйИљОнНЧЦНЗжЯпаджЪЃЌСаГіЗНГЬНтОіЮЪЬтЃЎ
ЃЈ2ЃЉгЩЁїQTMЁзЁїBCDЃЌЕУ![]() СаГіЗНГЬМДПЩНтОіЃЎ
СаГіЗНГЬМДПЩНтОіЃЎ
ЃЈ3ЃЉЂйШчЭМ2жаЃЌгЩДЫQMНЛCDгкEЃЌЧѓГіDEЁЂDOРћгУВюжЕБШНЯМДПЩНтОіЮЪЬтЃЎ
ЂкШчЭМ3жаЃЌгЩЂйПЩжЊЁбOжЛгадкзѓВргыжБЯпQMЯрЧагкЕуHЃЌQMгыCDНЛгкЕуEЃЎгЩЁїOHEЁзЁїBCDЃЌЕУ![]() ЃЌСаГіЗНГЬМДПЩНтОіЮЪЬтЃЎРћгУЗДжЄЗЈжЄУїжБЯпPMВЛПЩФмгЩЁбOЯрЧаЃЎ
ЃЌСаГіЗНГЬМДПЩНтОіЮЪЬтЃЎРћгУЗДжЄЗЈжЄУїжБЯпPMВЛПЩФмгЩЁбOЯрЧаЃЎ
ЃЈ1ЃЉНтЃКШчЭМ1жаЃЌЁпЫФБпаЮABCDЪЧОиаЮЃЌ
ЁрЁЯA=ЁЯC=ЁЯADC=ЁЯABC=90ЁуЃЌAB=CD=6ЃЎAD=BC=8ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁпPQЁЭBDЃЌ
ЁрЁЯBPQ=90Ёу=ЁЯCЃЌ
ЁпЁЯPBQ=ЁЯDBCЃЌ
ЁрЁїPBQЁзЁїCBDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрPQ=3tЃЌBQ=5tЃЌ
ЁпDQЦНЗжЁЯBDCЃЌQPЁЭDBЃЌQCЁЭDCЃЌ
ЁрQP=QCЃЌ
Ёр3t=8-5tЃЌ
Ёрt=1ЃЌ
ЙЪД№АИЮЊЃК1ЃЎ
ЃЈ2ЃЉНтЃКШчЭМ2жаЃЌзїMTЁЭBCгкTЃЎ
ЁпMC=MQЃЌMTЁЭCQЃЌ
ЁрTC=TQЃЌ
гЩЃЈ1ЃЉПЩжЊTQ=![]() ЃЈ8-5tЃЉЃЌQM=3tЃЌ
ЃЈ8-5tЃЉЃЌQM=3tЃЌ
ЁпMQЁЮBDЃЌ
ЁрЁЯMQT=ЁЯDBCЃЌ
ЁпЁЯMTQ=ЁЯBCD=90ЁуЃЌ
ЁрЁїQTMЁзЁїBCDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр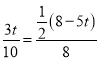 ЃЌ
ЃЌ
Ёрt=![]() ЃЈsЃЉЃЌ
ЃЈsЃЉЃЌ
Ёрt=![]() sЪБЃЌЁїCMQЪЧвдCQЮЊЕзЕФЕШбќШ§НЧаЮЃЎ
sЪБЃЌЁїCMQЪЧвдCQЮЊЕзЕФЕШбќШ§НЧаЮЃЎ
ЃЈ3ЃЉЂйжЄУїЃКШчЭМ2жаЃЌгЩДЫQMНЛCDгкEЃЌ
ЁпEQЁЮBDЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрEC=![]() ЃЈ8-5tЃЉЃЌED=DC-EC=6-
ЃЈ8-5tЃЉЃЌED=DC-EC=6-![]() ЃЈ8-5tЃЉ=
ЃЈ8-5tЃЉ=![]() tЃЌ
tЃЌ
ЁпDO=3tЃЌ
ЁрDE-DO=![]() t-3t=
t-3t=![]() tЃО0ЃЌ
tЃО0ЃЌ
ЁрЕуOдкжБЯпQMзѓВрЃЎ
ЂкНтЃКШчЭМ3жаЃЌгЩЂйПЩжЊЁбOжЛгадкзѓВргыжБЯпQMЯрЧагкЕуHЃЌQMгыCDНЛгкЕуEЃЎ
ЁпEC=![]() ЃЈ8-5tЃЉЃЌDO=3tЃЌ
ЃЈ8-5tЃЉЃЌDO=3tЃЌ
ЁрOE=6-3t-![]() ЃЈ8-5tЃЉ=
ЃЈ8-5tЃЉ=![]() tЃЌ
tЃЌ
ЁпOHЁЭMQЃЌ
ЁрЁЯOHE=90ЁуЃЌ
ЁпЁЯHEO=ЁЯCEQЃЌ
ЁрЁЯHOE=ЁЯCQE=ЁЯCBDЃЌ
ЁпЁЯOHE=ЁЯC=90ЁуЃЌ
ЁрЁїOHEЁзЁїBCDЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр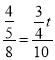 ЃЌ
ЃЌ
Ёрt=![]() ЃЎ
ЃЎ
Ёрt=![]() sЪБЃЌЁбOгыжБЯпQMЯрЧаЃЎ
sЪБЃЌЁбOгыжБЯпQMЯрЧаЃЎ
СЌНгPMЃЌМйЩшPMгыЁбOЯрЧаЃЌдђЁЯOMH=![]() PMQ=22.5ЁуЃЌ
PMQ=22.5ЁуЃЌ
дкMHЩЯШЁвЛЕуFЃЌЪЙЕУMF=FOЃЌдђЁЯFMO=ЁЯFOM=22.5ЁуЃЌ
ЁрЁЯOFH=ЁЯFOH=45ЁуЃЌ
ЁрOH=FH=![]() ЃЌFO=FM=
ЃЌFO=FM=![]() ЃЌ
ЃЌ
ЁрMH=![]() ЃЈ
ЃЈ![]() +1ЃЉЃЌ
+1ЃЉЃЌ
гЩ![]() ЕУЕНHE=
ЕУЕНHE=![]() ЃЌ
ЃЌ
гЩ![]() ЕУЕНEQ=
ЕУЕНEQ=![]() ЃЌ
ЃЌ
ЁрMH=MQ-HE-EQ=4-![]() -
-![]() =
=![]() ЃЌ
ЃЌ
Ёр![]() ЃЈ
ЃЈ![]() +1ЃЉЁй
+1ЃЉЁй![]() ЃЌУЌЖмЃЌ
ЃЌУЌЖмЃЌ
ЁрМйЩшВЛГЩСЂЃЎ
ЁржБЯпPMгыЁбOВЛЯрЧаЃЎ
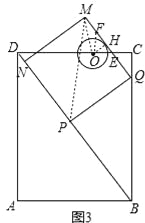
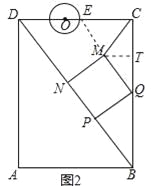



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌвбжЊЁїABCЕФШ§ИіЖЅЕузјБъЗжБ№ЪЧAЃЈ1ЃЌ1ЃЉЃЌBЃЈ4ЃЌ1ЃЉЃЌCЃЈ3ЃЌ3ЃЉЃЎ
ЃЈ1ЃЉНЋЁїABCЯђЯТЦНвЦ5ИіЕЅЮЛКѓЕУЕНЁїA1B1C1ЃЌЧыЛГіЁїA1B1C1ЃЛ
ЃЈ2ЃЉНЋЁїABCШЦдЕуOФцЪБеыа§зЊ90ЁуКѓЕУЕНЁїA2B2C2ЃЌЧыЛГіЁїA2B2C2ЃЛ
ЃЈ3ЃЉХаЖЯвдOЃЌA1ЃЌBЮЊЖЅЕуЕФШ§НЧаЮЕФаЮзДЃЎЃЈЮоаыЫЕУїРэгЩЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌвбжЊBЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЎ
ЃЈaЁй0ЃЉЕФЭМЯѓгыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкCЕуЃЌвбжЊBЕузјБъЮЊЃЈ4ЃЌ0ЃЉЃЎ
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЪдЬНОПЁїABCЕФЭтНгдВЕФдВаФЮЛжУЃЌВЂЧѓГідВаФзјБъЃЛ
ЃЈ3ЃЉШєЕуMЪЧЯпЖЮBCЯТЗНЕФХзЮяЯпЩЯвЛЕуЃЌЧѓЁїMBCЕФУцЛ§ЕФзюДѓжЕЃЌВЂЧѓГіДЫЪБMЕуЕФзјБъЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯп![]() ЃЌЕу
ЃЌЕу![]() дкжБЯп
дкжБЯп![]() ЩЯЃЌвдЕу
ЩЯЃЌвдЕу![]() ЮЊдВаФЃЌЪЪЕБГЄЮЊАыОЖЛЛЁЃЌЗжБ№НЛжБЯп
ЮЊдВаФЃЌЪЪЕБГЄЮЊАыОЖЛЛЁЃЌЗжБ№НЛжБЯп![]() гкЕу
гкЕу![]() ЃЌСЌНг
ЃЌСЌНг![]() . Шє
. Шє![]() ЃЌдђ
ЃЌдђ![]() ЕФЖШЪ§ЮЊ____________.
ЕФЖШЪ§ЮЊ____________.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
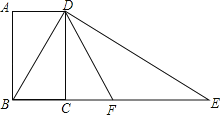
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЮЊОиаЮЃЌЙ§ЕуDзїЖдНЧЯпBDЕФДЙЯпЃЌНЛBCЕФбгГЄЯпгкЕуEЃЌШЁBEЕФжаЕуFЃЌСЌНгDFЃЌDF=4ЃЎЩшAB=xЃЌAD=yЃЌдђx2+ЃЈyЉ4ЃЉ2ЕФжЕЮЊ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDЕФБпГЄЮЊ2ЃЌЕуE.FЗжБ№дкБпADЁЂCDЩЯЃЌЁЯEBF=45ЁуЃЌдђЁїEDF
ЕФжмГЄЕШгк_______ЁЃ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮ![]() жаЕФШ§ИіЖЅЕудкЁб
жаЕФШ§ИіЖЅЕудкЁб![]() ЩЯЃЌ
ЩЯЃЌ![]() ЪЧгХЛЁ
ЪЧгХЛЁ![]() ЩЯЕФвЛИіЖЏЕу(ВЛгыЕу
ЩЯЕФвЛИіЖЏЕу(ВЛгыЕу![]() ЁЂ
ЁЂ![]() жиКЯ).
жиКЯ).
(1)ЕБдВаФ![]() дк
дк![]() ФкВПЃЌ
ФкВПЃЌ![]() ЪБЃЌ
ЪБЃЌ![]() ________.
________.
(2)ЕБдВаФ![]() дк
дк![]() ФкВПЃЌЫФБпаЮ
ФкВПЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЪБЃЌЧѓ
ЮЊЦНааЫФБпаЮЪБЃЌЧѓ![]() ЕФЖШЪ§;
ЕФЖШЪ§;
(3)ЕБдВаФ![]() дк
дк![]() ЭтВПЃЌЫФБпаЮ
ЭтВПЃЌЫФБпаЮ![]() ЮЊЦНааЫФБпаЮЪБЃЌЧыжБНгаДГі
ЮЊЦНааЫФБпаЮЪБЃЌЧыжБНгаДГі![]() гы
гы![]() ЕФЪ§СПЙиЯЕ.
ЕФЪ§СПЙиЯЕ.

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдНРДдНЖрЕФШЫдкгУЮЂаХИЖПюЁЂзЊеЫЃЌАбЮЂаХеЫЛЇРяЕФЧЎзЊЕНвјааПЈНазіЬсЯжЁЃ
зд2016Фъ3дТlШеЦ№ЃЌУПИіЮЂаХеЫЛЇжеЩэЯэга1000дЊЕФУтЗбЬсЯжЖюЖШЃЌЕБРлМЦЬсЯжН№ЖюГЌЙ§1000дЊЪБЃЌРлМЦЬсЯжН№ЖюГЌГі1000дЊЕФВПЗжашжЇИЖ0.1%ЕФЪжајЗбЃЌвдКѓУПДЮЬсЯжжЇИЖЕФЪжајЗбЮЊЬсЯжН№ЖюЕФ0.1%.
ЃЈ1ЃЉаЁУїдкНёЬьЕк1ДЮНјааСЫЬсЯжЃЌН№ЖюЮЊl600дЊЃЌЫћашжЇИЖЪжајЗб_________дЊЃЛ
ЃЈ2ЃЉаЁССзд2016Фъ3дТ1ШежСНёЃЌгУздМКЕФЮЂаХеЫЛЇЙВЬсЯж3ДЮЃЌ3ДЮЬсЯжН№ЖюКЭЪжајЗбЗжБ№ШчЯТЃК
Ек1ДЮ | Ек2ДЮ | Ек3ДЮ | |
ЬсЯжН№ЖюЃЈдЊЃЉ | A | b |
|
ЪжајЗбЃЈдЊЃЉ | 0 | 0.4 | 3.4 |
ЮЪЃКаЁУї3ДЮЬсЯжН№ЖюИїЪЧЖрЩйдЊЃП
ЃЈ3ЃЉЕЅБЪЪжајЗбаЁгк0.1дЊЕФЃЌАДее0.1дЊЪеШЁЃЈМДЬсЯжВЛзу100дЊЃЌАДее100дЊЪеШЁЪжајЗбЃЉ.аЁКьжСНёЙВЬсЯжСНДЮЃЌУПДЮЬсЯжН№ЖюЖМЪЧећЪ§ЃЌЙВжЇИЖЪжајЗб2.4дЊЃЌЕквЛДЮЬсЯж900дЊЁЃЧѓаЁКьЕкЖўДЮЬсЯжН№ЖюЕФЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com