
【题目】如图,把△EFP放置在菱形ABCD中,使得顶点E,F,P分别在线段AB,AD,AC上,已知EP=FP=6,EF=![]() ,∠BAD=60°,且AB>
,∠BAD=60°,且AB>![]() .
.
(1)求∠EPF的大小;
(2)若AP=10,求AE+AF的值;
(3)若△EFP的三个顶点E、F、P分别在线段AB、AD、AC上运动,请直接写出AP长的最大值和最小值.
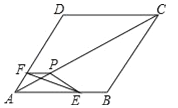
【答案】(1)120°;(2)![]() ;(3)AP的最大值为12,AP的最小值为6.
;(3)AP的最大值为12,AP的最小值为6.
【解析】
试题分析:(1)根据锐角三角函数求出∠FPG,最后求出∠EPF.
(2)先判断出Rt△PME≌Rt△PNF,再根据锐角三角函数求解即可,(3)根据运动情况及菱形的性质判断求出AP最大和最小值.
试题解析:(1)过点P作PG⊥EF于点G,如图1所示.
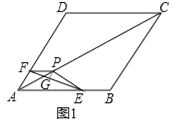
∵PE=PF=6,EF![]() ,∴FG=EG=
,∴FG=EG=![]() ,∠FPG=∠EPG=
,∠FPG=∠EPG=![]() ∠EPF.
∠EPF.
在Rt△FPG中,sin∠FPG=![]() =
=![]() =
=![]() ,∴∠FPG=60°,∴∠EPF=120°;
,∴∠FPG=60°,∴∠EPF=120°;
(2)过点P作PM⊥AB于点M,作PN⊥AD于点N,如图2所示.
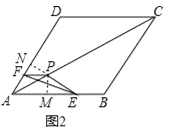
∵AC为菱形ABCD的对角线,∴∠DAC=∠BAC,AM=AN,PM=PN.
在Rt△PME和Rt△PNF中,PM=PN,PE=PF,∴Rt△PME≌Rt△PNF,∴ME=NF.
又AP=10,∠PAM=![]() ∠DAB=30°,∴AM=AN=APcos30°=10×
∠DAB=30°,∴AM=AN=APcos30°=10×![]() =
=![]() ,∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=
,∴AE+AF=(AM+ME)+(AN﹣NF)=AM+AN=![]() ;
;
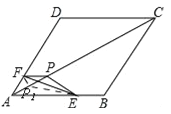
(3)如图,当△EFP的三个顶点分别在AB,AD,AC上运动,点P在P1,P之间运动,∴P1O=PO=3,AO=9,∴AP的最大值为12,AP的最小值为6.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点B(6,0)的直线AB与直线OA相交于点A(4,2),动点M沿路线O→A→C运动. 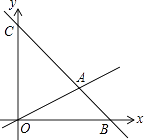
(1)求直线AB的解析式.
(2)求△OAC的面积.
(3)当△OMC的面积是△OAC的面积的 ![]() 时,求出这时点M的坐标.
时,求出这时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;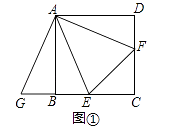
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;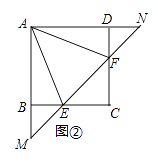
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.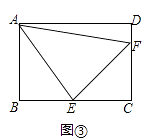
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com