
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
【答案】(1)①证明见解析;②BE2+CF2=EF2;(2)①②④.
【解析】试题分析:(1)①可按阅读理解中的方法构造全等,把CF和BE转移到一个三角形中,利用三角形的三边关系求解即可;②由∠A=90°,可得∠EBC+∠FCB=90°,由①中的全等得到∠C=∠CBG;即可得∠ABC+∠CBG =90°,即∠EBG=90°,由此可得可得三边之间存在勾股定理关系;(2)①在ABCD中,AD=2AB,F是AD的中点,可得AF=FD=CD,即可得∠DFC=∠DCF;再由AD∥BC,根据平行线的性质可得∠DFC=∠FCB,所以∠DCF=∠BCF,根据角平分线的定义可得∠DCF=![]() ∠BCD,①正确;②延长EF,交CD延长线于M,根据已知条件易证△AEF≌△DMF,根据全等三角形的性质可得FE=MF,∠AEF=∠M,又因CE⊥AB,可得∠AEC=90°,所以∠AEC=∠ECD=90°,因FM=EF,根据直角三角形斜边上的中线等于斜边的一半可得FC=FM,②正确;③由EF=FM可得S△EFC=S△CFM,又因MC>BE,即可得S△BEC<2S△EFC,所以S△BEC=2S△CEF错误,即③错误;④设∠FEC=x,则∠FCE=x,所以∠DCF=∠DFC=90°﹣x,根据三角形外角的性质可得∠EFC=180°﹣2x,所以∠EFD=90°﹣x+180°﹣2x=270°﹣3x,再由∠AEF=90°﹣x,即可得∠DFE=3∠AEF,④正确.
∠BCD,①正确;②延长EF,交CD延长线于M,根据已知条件易证△AEF≌△DMF,根据全等三角形的性质可得FE=MF,∠AEF=∠M,又因CE⊥AB,可得∠AEC=90°,所以∠AEC=∠ECD=90°,因FM=EF,根据直角三角形斜边上的中线等于斜边的一半可得FC=FM,②正确;③由EF=FM可得S△EFC=S△CFM,又因MC>BE,即可得S△BEC<2S△EFC,所以S△BEC=2S△CEF错误,即③错误;④设∠FEC=x,则∠FCE=x,所以∠DCF=∠DFC=90°﹣x,根据三角形外角的性质可得∠EFC=180°﹣2x,所以∠EFD=90°﹣x+180°﹣2x=270°﹣3x,再由∠AEF=90°﹣x,即可得∠DFE=3∠AEF,④正确.
试题解析:
延长FD到G,使得DG=DF,连接BG、EG.(或把△CFD绕点D逆时针旋转180°得到△BGD),
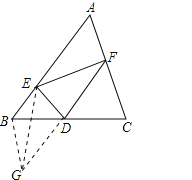
∵BD=CD,∠BDG=∠CDF,
∴△BDG≌△CDF,
∴CF=BG,
∵DE⊥DF,DF=DG,
∴EF=EG.
在△BEG中,BE+BG>EG,即BE+CF>EF.
②若∠A=90°,则∠EBC+∠FCB=90°,
由①知∠FCD=∠DBG,EF=EG,
∴∠EBC+∠DBG=90°,即∠EBG=90°,
∴在Rt△EBG中,BE2+BG2=EG2,
∴BE2+CF2=EF2;
(2)①∵F是AD的中点,
∴AF=FD,
∵在ABCD中,AD=2AB,
∴AF=FD=CD,
∴∠DFC=∠DCF,
∵AD∥BC,
∴∠DFC=∠FCB,
∴∠DCF=∠BCF,
∴∠DCF=![]() ∠BCD,故此选项正确;
∠BCD,故此选项正确;
②延长EF,交CD延长线于M,
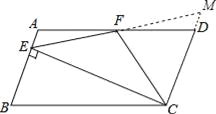
∵四边形ABCD是平行四边形,
∴AB∥CD,
∴∠A=∠MDF,
∵F为AD中点,
∴AF=FD,
在△AEF和△DFM中, 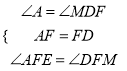 ,
,
∴△AEF≌△DMF(ASA),
∴FE=MF,∠AEF=∠M,
∵CE⊥AB,
∴∠AEC=90°,
∴∠AEC=∠ECD=90°,
∵FM=EF,
∴FC=FM,故②正确;
③∵EF=FM,
∴S△EFC=S△CFM,
∵MC>BE,
∴S△BEC<2S△EFC
故S△BEC=2S△CEF错误;
④设∠FEC=x,则∠FCE=x,
∴∠DCF=∠DFC=90°﹣x, ∴∠EFC=180°﹣2x, ∴∠EFD=90°﹣x+180°﹣2x=270°﹣3x, ∵∠AEF=90°﹣x, ∴∠DFE=3∠AEF,故此选项正确. 故正确答案为:①②④.


科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点D,E分别在边BC,AC上,且DE∥AB,过点E作EF⊥DE,交BC的延长线于点F.
(1)求∠F的度数;
(2)若CD=2,求DF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读理解:课外兴趣小组活动时,老师提出了如下问题:
如图1,△ABC中,若AB=5,AC=3,求BC边上的中线AD的取值范围.
小明在组内经过合作交流,得到了如下的解决方法:延长AD到E,使得DE=AD,再连接BE(或将△ACD绕点D逆时针旋转180°得到△EBD),把AB、AC、2AD集中在△ABE中,利用三角形的三边关系可得2<AE<8,则1<AD<4.
感悟:解题时,条件中若出现“中点”“中线”字样,可以考虑构造以中点为对称中心的中心对称图形,把分散的已知条件和所求证的结论集中到同一个三角形中.
(1)问题解决:受到(1)的启发,请你证明下面命题:如图2,在△ABC中,D是BC边上的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,连接EF.
①求证:BE+CF>EF;②若∠A=90°,探索线段BE、CF、EF之间的等量关系,并加以证明;
(2)问题拓展:如图3,在平行四边形ABCD中,AD=2AB,F是AD的中点,作CE⊥AB,垂足E在线段AB上,联结EF、CF,那么下列结论①∠DCF=![]() ∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).
∠BCD;②EF=CF;③S△BEC=2S△CEF;④∠DFE=3∠AEF.中一定成立是 (填序号).


图1 图2 图3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】认真阅读下面关于三角形内外角平分线所夹角的探究片段,完成所提出的问题.
探究1:如图l,在△ABC中,O是∠ABC与∠ACB的平分线BO和CO的交点,通过分析发现∠BOC=90![]() +
+![]() ∠A,理由如下:
∠A,理由如下:
∵BO和CO分别是∠ABC和∠ACB的角平分线
∴∠1=![]() ∠ABC, ∠2=
∠ABC, ∠2=![]() ∠ACB
∠ACB
∴∠l+∠2=![]() (∠ABC+∠ACB)=
(∠ABC+∠ACB)= ![]() (180
(180![]() -∠A)= 90
-∠A)= 90![]() -
-![]() ∠A
∠A
∴∠BOC=180![]() -(∠1+∠2) =180
-(∠1+∠2) =180![]() -(90
-(90![]() -
-![]() ∠A)=90
∠A)=90![]() +
+![]() ∠A
∠A
(1)探究2;如图2中,O是![]() ∠ABC与外角
∠ABC与外角![]() ∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
∠ACD的平分线BO和CO的交点,试分析∠BOC与∠A有怎样的关系?请说明理由.
(2)探究3:如图3中, O是外角∠DBC与外角∠ECB的平分线BO和CO的交点,则∠BOC与∠A有怎样的关系?(直接写出结论)
(3)拓展:如图4,在四边形ABCD中,O是∠ABC与∠DCB的平分线BO和CO的交点,则∠BOC与∠A+∠D有怎样的关系?(直接写出结论)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,在ABCD中,AB=3cm,BC=5cm,AC⊥AB,△ACD沿射线AC的方向匀速平移得到△PNM,速度为1cm/s,同时,点Q从点C出发,沿射线CB方向匀速运动,速度为1cm/s,当△PNM停止平移时,点Q也停止运动,如图2所示,设运动时间为t(s)(0<t<4).
(1)当t为何值时,PQ∥MN?
(2)设△QMC的面积为y(cm2),求y与t之间的函数关系式;
(3)是否存在某一时刻t,使得PQ=QM,若存在,求出t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】养成良好的早锻炼习惯,对学生的学习和生活非常有益![]() 某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间
某中学为了了解七年级学生的早锻炼情况,校政教处在七年级随机抽取了部分学生,并对这些学生通常情况下一天的早锻炼时间![]() 分钟
分钟![]() 进行了调查
进行了调查![]() 现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.
现把调查结果分为A,B,C,D四组,如下表所示;同时,将调查结果绘制成下面两幅不完整的统计图.

组别 | 早锻炼时间 |
A |
|
B |
|
C |
|
D |
|
请根据以上提供的信息,解答下列问题:
![]() 扇形统计图中D所在扇形的圆心角度数为______;
扇形统计图中D所在扇形的圆心角度数为______;
![]() 补全频数分布直方图;
补全频数分布直方图;
![]() 已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
已知该校七年级共有1200名学生,请你估计这个年级学生中有多少人一天早锻炼的时间不少于20分钟.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图∠1=∠2,CF⊥AB,DE⊥AB,求证:FG∥BC.
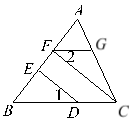
证明:∵CF⊥AB,DE⊥AB (已知)
∴∠BED=90°,∠BFC=90°( )
∴∠BED=∠BFC ( )
∴ED∥FC ( )
∴∠1=∠BCF ( )
∵∠2=∠1 ( 已知 )
∴∠2=∠BCF ( )
∴FG∥BC ( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是一张平行四边形纸片ABCD,要求利用所学知识将它变成一个菱形,甲、乙两位同学的作法分别如下:

对于甲、乙两人的作法,可判断( )
A. 甲正确,乙错误 B. 甲错误,乙正确
C. 甲、乙均正确 D. 甲、乙均错误
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com