Question

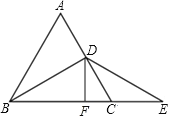
【题目】如图，△ABC是等边三角形，BD是中线，延长BC至E，CE=CD，

（1）求证：DB=DE．

（2）在图中过D作DF⊥BE交BE于F，若CF=4，求△ABC的周长．

Answer 1

【答案】（1）证明见解析（2）48

【解析】试题分析：（1）根据等边三角形的性质得到∠ABC=∠ACB=60°，∠DBC=30°，再根据角之间的关系求得∠DBC=∠CED，根据等角对等边即可得到DB=DE；（2）根据直角三角形中，30°的锐角所对的直角边等于斜边的一半DC=8，AC=16，即可求得△ABC的周长．

试题解析：

（1）证明：∵△ABC是等边三角形，BD是中线，

∴∠ABC=∠ACB=60°．

∠DBC=30°（等腰三角形三线合一）．

又∵CE=CD，

∴∠CDE=∠CED．

又∵∠BCD=∠CDE+∠CED，

∴∠CDE=∠CED=∠BCD=30°．

∴∠DBC=∠DEC．

∴DB=DE（等角对等边）；

（2）解： ∵∠CDE=∠CED=∠BCD=30°，

∴∠CDF=30°，

∵CF=4，

∴DC=8，

∵AD=CD，

∴AC=16，

∴△ABC的周长=3AC=48．