
分析 (1)根据利润=总额-成本列出代数式;
(2)把m=0.5元,n=1.1元代入(1)中所列的代数式并解答,然后比较;
(3)根据题意列出关于m的方程,通过解方程可以得到m的值.
解答 解:(1)方式一:出售大白菜的纯收入为18000m-5000,
方式二:18000÷1000=18(天),
则出售大白菜的纯收入为:1000n×18-5000-200×18-100×18=18000n-10400;
(2)方式一的出售获利较多.理由如下:
方式一:把m=0.5元代入18000m-5000,得到:18000×0.5-5000=4000(元).
方式二:把n=1.1元代入18000n-10400,得到:18000×1.1-10400=9400(元).
因为4000<9400,
所以方式二的出售获利较多.
(3)依题意得:18000m-5000=18000n-10400,
整理,得
10n-10m=3,
把n=1.2代入,得
12-10m=3,
解得m=0.9.
答:当n=1.2元,m为0.9元时,两种方式获利一样.
点评 本题考查了列代数式,代数式求值,以及一元一次方程的应用.解题关键是要读懂题目的意思,根据题目给出的条件,找出合适的等量关系列出方程,再求解.


 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案科目:初中数学 来源: 题型:解答题
 如图,将一块长50厘米、宽40厘米的铁皮剪去四个正方形的角,就可以折成一个长方体无盖盒子.如果盒子的底面积为600平方厘米,求盒子的高度.
如图,将一块长50厘米、宽40厘米的铁皮剪去四个正方形的角,就可以折成一个长方体无盖盒子.如果盒子的底面积为600平方厘米,求盒子的高度.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
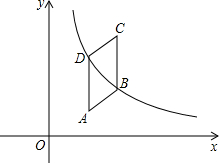 如图,在?ABCD中,AB⊥BD,sinA=$\frac{4}{5}$,将?ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=$\frac{k}{x}$(k>0)同时经过B、D两点,则点B的坐标是($\frac{9}{5}$,$\frac{4}{3}$).
如图,在?ABCD中,AB⊥BD,sinA=$\frac{4}{5}$,将?ABCD放置在平面直角坐标系中,且AD⊥x轴,点D的横坐标为1,点C的纵坐标为3,恰有一条双曲线y=$\frac{k}{x}$(k>0)同时经过B、D两点,则点B的坐标是($\frac{9}{5}$,$\frac{4}{3}$).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 己知如图,在梯形ABCD中,AB∥CD.AC、BD为对角线,MN∥CB.且与AB、DC分别相交于点M、N.与DB、AC分别相交于点P、Q.
己知如图,在梯形ABCD中,AB∥CD.AC、BD为对角线,MN∥CB.且与AB、DC分别相交于点M、N.与DB、AC分别相交于点P、Q.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3 | B. | -3 | C. | 3(b-a) | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在矩形ABCD中,AB<AD,AF⊥BD于点E,交BC于点F,连接DF,则下列结论错误的是( )
如图,在矩形ABCD中,AB<AD,AF⊥BD于点E,交BC于点F,连接DF,则下列结论错误的是( )| A. | △ABC≌△CDB | B. | S△ABD=S△ADF | C. | ∠ADB=∠CDF | D. | ∠DBF>∠BDF |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
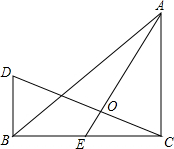 如图,在△ABC中,∠ACB=90°,AC=BC,DB⊥BC于点B,点E在BC上,AE、CD相交于点O,当AE与CD满足怎样的数量关系时,AE⊥CD,并说明理由.
如图,在△ABC中,∠ACB=90°,AC=BC,DB⊥BC于点B,点E在BC上,AE、CD相交于点O,当AE与CD满足怎样的数量关系时,AE⊥CD,并说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y=-x2-6x+9 | B. | y=2x2-x+1 | C. | y=-x2+2x-5 | D. | y=2x2-4x+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com