
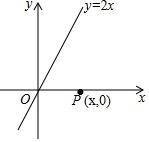 如图,已知直线y=2x和x轴上一动点P(x,0).
如图,已知直线y=2x和x轴上一动点P(x,0).分析 (1)根据点到直线的距离公式,可得答案;
(2)根据点到直线的距离公式,可得答案.
解答 解:(1)直线的解析式为2x-y=0,
P到直线的距离为$\frac{|2x-0|}{\sqrt{{2}^{2}+(-1)^{2}}}$=2,
解得x=$\sqrt{5}$或x=-$\sqrt{5}$,
P点坐标为($\sqrt{5}$,0)或(-$\sqrt{5}$,0);
(2)平移后的解析式为y=2x+1,
2x-y+1=0,
P到直线的距离为$\frac{|2x-0+1|}{\sqrt{{2}^{2}+(-1)^{2}}}$=m,
m=$\frac{2\sqrt{5}}{5}$x或m=-$\frac{2\sqrt{5}}{5}$x.
点评 本题考查了一次函数图象与几何变换,解(1)的关键是利用点到直线的距离公式;解(2)的关键是利用函数图象的平移规律,又利用了点到直线的距离公式.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 甲种机器 | 乙种机器 | |
| 价格/(万元/台) | 5 | 7 |
| 每台机器的日生产量/个 | 60 | 100 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
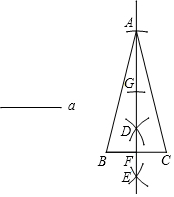 下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.
下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com