
【题目】小强在教学楼的点P处观察对面的办公大楼.为了测量点P到对面办公大楼上部AD的距离,小强测得办公大楼顶部点A的仰角为45°,测得办公大楼底部点B的俯角为60°,已知办公大楼高46米,CD=10米.求点P到AD的距离(用含根号的式子表示).
【答案】解:连接PA、PB,过点P作PM⊥AD于点M;延长BC,交PM于点N
则∠APM=45°,∠BPM=60°,NM=10米
设PM=x米
在Rt△PMA中,AM=PM×tan∠APM=xtan45°=x(米)
在Rt△PNB中,BN=PN×tan∠BPM=(x﹣10)tan60°=(x﹣10) ![]() (米)
(米)
由AM+BN=46米,得x+(x﹣10) ![]() =46
=46
解得, ![]() =18
=18 ![]() ﹣8,
﹣8,
∴点P到AD的距离为 ![]() 米.
米.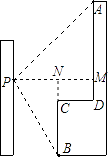
【解析】连接PA、PB,过点P作PM⊥AD于点M;延长BC,交PM于点N,将实际问题中的已知量转化为直角三角形中的有关量,设PM=x米,在Rt△PMA中,表示出AM,在Rt△PNB中,表示出BN,由AM+BN=46米列出方程求解即可.
【考点精析】根据题目的已知条件,利用勾股定理的概念的相关知识可以得到问题的答案,需要掌握直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.


科目:初中数学 来源: 题型:
【题目】如图,已知直线CB∥OA,∠C=∠OAB=100°,点E、F在线段BC上,满足∠FOB=∠AOB=α,OE平分∠COF.
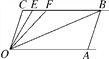
(1)用含有α的代数式表示∠COE的度数;
(2)若沿水平方向向右平行移动AB,则∠OBC∶∠OFC的值是否发生变化?若变化,找出变化规律;若不变,求其比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年,新疆某次足球联赛规定每队胜一场得3分,平一场得1分,负一场得0分,某队前14场保持不败,共得32分,设该队平了x场,根据题意列方程得:_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,O为矩形ABCD的中心,M为BC边上一点,N为DC边上一点,ON⊥OM,若AB=6,AD=4,设OM=x,ON=y,则y与x的函数关系式为 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】北京奥运会体育场的“鸟巢”钢结构工程施工建设中,首次使用了我国科研人员自主研制的强度为4.6×108帕的钢材,那么它的原数是( )
A.4600000B.46000000C.460000000D.4600000000
查看答案和解析>>
科目:初中数学 来源: 题型:
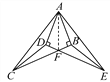
【题目】如图,∠ABC=∠ADE=90°,AD=AB,AC=AE,BC与DE相交于点F,连接CD、EB.
(1)图中共有几对全等三角形,请你一一列举;
(2)求证:CF=EF.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雅安地震发生后,全国人民抗震救灾,众志成城,值地震发生一周年之际,某地政府又筹集了重建家园的必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型 | 甲 | 乙 | 丙 |
汽车运载量(吨/辆) | 5 | 8 | 10 |
汽车运费(元/辆) | 400 | 500 | 600 |
(1)全部物资可用甲型车8辆,乙型车5辆,丙型车 辆来运送.
(2)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(3)为了节省运费,该地政府打算用甲、乙、丙三种车型同时参与运送,已知它们的总辆数为14辆,你能分别求出三种车型的辆数吗?此时的运费又是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】文文和彬彬在证明“有两个角相等的三角形是等腰三角形”这一命题时,画出图形,写出“已知”,“求证”(如图),她们对各自所作的辅助线描述如下:

文文:“过点A作BC的中垂线AD,垂足为D”;
彬彬:“作△ABC的角平分线AD”.
数学老师看了两位同学的辅助线作法后,说:“彬彬的作法是正确的,而文文的作法需要订正.”
(1)请你简要说明文文的辅助线作法错在哪里;
(2)根据彬彬的辅助线作法,完成证明过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O1、⊙O2相交于P、Q两点,其中⊙O1的半径r1=2,⊙O2的半径r2= ![]() .过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C、D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A、B,连接AP、BP、AC、DB,且AC与DB的延长线交于点E.
.过点Q作CD⊥PQ,分别交⊙O1和⊙O2于点C、D,连接CP、DP,过点Q任作一直线AB交⊙O1和⊙O2于点A、B,连接AP、BP、AC、DB,且AC与DB的延长线交于点E. 
(1)求证: ![]() ;
;
(2)若PQ=2,试求∠E度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com