
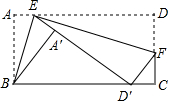
 如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.
如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$. 分析 如图,作EH⊥BC于H.设AE=x,则易知ED=ED′=BD′,设ED=BDED′=y,在Rt△EHD′中,y2=22+(y-x)2,可得y=$\frac{4+{x}^{2}}{2x}$=$\frac{2}{x}$+$\frac{1}{2}$x,推出AD=x+y=$\frac{3}{2}$x+$\frac{2}{x}$≥2$\sqrt{\frac{3}{2}x•\frac{2}{x}}$,由此即可解决问题.
解答 解: 如图,作EH⊥BC于H.设AE=x,则易知ED=ED′=BD′,设ED=BDED′=y,
如图,作EH⊥BC于H.设AE=x,则易知ED=ED′=BD′,设ED=BDED′=y,
在Rt△EHD′中,y2=22+(y-x)2,
∴y=$\frac{4+{x}^{2}}{2x}$=$\frac{2}{x}$+$\frac{1}{2}$x,
∴AD=x+y=$\frac{3}{2}$x+$\frac{2}{x}$≥2$\sqrt{\frac{3}{2}x•\frac{2}{x}}$,(a+b≥2$\sqrt{ab}$,a>0,b>0)
∴AD≥2$\sqrt{3}$,
∴AD的最小值为2$\sqrt{3}$.
故答案为2$\sqrt{3}$.
点评 本题考查翻折变换、勾股定理、矩形的性质、不等式的性质等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题,记住a+b≥2$\sqrt{ab}$,a>0,b>0,这个基本不等式.


科目:初中数学 来源: 题型:选择题
| A. | 0.788×108 | B. | 7.88×108 | C. | 7.88×109 | D. | 788×106 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | 500 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.
如图,已知A(-4,n),B(2,-4)是一次函数y=kx+b和反比例函数y=$\frac{m}{x}$的图象的两个交点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com