
 下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:
下表1为抄录北京奥运会官方票务网公布的三种球类比赛的部分门票价格,如图是按照某公司购买的100张门票的种类、数量绘制的扇形图:| 比赛项目 | 票价(元/张) |
| 足球 | 1000 |
| 男篮 | 800 |
| 乒乓球 | 500 |
分析 (1)求观看乒乓球比赛的门票占全部门票的分率,把全部门票看做单位“1”,用1-50%-30%解答;求观看足球比赛的门票有多少张:用总张数100乘50%即可;
(2)分别求出三种球票各买了多少张,然后求出一共花了多少钱,用乒乓球门票的总款数除以全部门票总款数即可;
(3)①把第二周的门票销售额为200万元看作单位“1”,用乘法求出第三周的门票销售额;
②把第一周销售额看作单位“1”,用除法求出第一周的门票销售额.
解答 解:(1)1-30%-50%=20%,
100×50%=50(张),
答:其中观看乒乓球比赛的门票占全部门票的 20%;看足球比赛的门票有 50张;
故答案为:20,50;
(2)100×50%=50(张),
100×30%=30(张),
100×20%=20(张),
1000×50=50000(元),
800×30=24000(元),
500×20=10000(元),
∴10000÷(50000+24000+10000)
=10000÷84000
=$\frac{5}{42}$,
答:购买乒乓球门票的总款数占全部门票总款数的 $\frac{5}{42}$;
故答案为:$\frac{5}{42}$;
(3)①200×(1+6%+4%)=220(万元),
故这个售票点第三周的门票销售额为220万元;
②200÷(1+6%),
=200÷1.06,
≈189(万元),
故这个售票点第一周的门票销售额为189万元.
答:这个售票点第三周的门票销售额为220万元.这个售票点第一周的门票销售额为189万元.
点评 本题主要考查了扇形统计图的应用,解题时注意:通过扇形统计图可以很清楚地表示出各部分数量同总数之间的关系.用整个圆的面积表示总数(单位1),用圆的扇形面积表示各部分占总数的百分数.


 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案科目:初中数学 来源: 题型:选择题
| A. | 1.901×106人 | B. | 19.01×105 人 | C. | 190.1×104人 | D. | 1901×103人 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
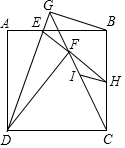 如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.
如图,E为正方形ABCD边AB上的一点,且AD=3,AE=1,将△ADE沿DE翻折得到△FDE,连接并延长CF与DE延长线相交于点G,连接BG,延长EF交BC于H,过点H作HI∥BG,则HI的长为$\frac{3}{10}$$\sqrt{10}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
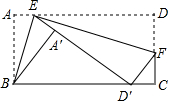 如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.
如图,矩形纸片ABCD中,AB=2,E为AD边上一点,先沿BE折叠纸片,点A落在矩形内部A'处,再沿EF折叠纸片,使点D落在边BC上D'处(不与点A'重合),旦E、A'、D'三点在一条直线上,则AD的长的最小值为2$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则AD的长为( )
如图,在△ABC中,∠C=90°,AC=4,BC=3,将△ABC绕点A逆时针旋转,使点C落在线段AB上的点E处,点B落在点D处,则AD的长为( )| A. | 3 | B. | 4 | C. | 5 | D. | $\sqrt{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com