
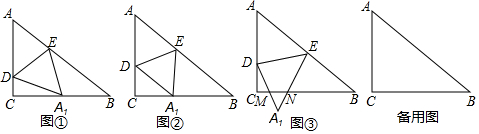
���� ��1����Rt��A1CD�У����ݹ��ɶ����ã�x2+42=��6-x��2����x��ֵ����CD�ij���
��2����ͼ�ڣ����۵��ã�A1D=AD=$\frac{15}{4}$�����ù��ɶ����ã�A1C=$\sqrt{��\frac{15}{4}��^{2}-��\frac{9}{4}��^{2}}$=3��֤����CA1D�ס�CBA�����ö�Ӧ����Ⱥ�ƽ���ߵ��ж���֤���ı���ADA1E��ƽ���ı��Σ��ټ���һ���ڱ���ȿɵý��ۣ�
��3������ͼ�ۣ��������߹�����ƽ���ߣ���PQ��AQ�ij�������ͬ�ǵ����Ǻ����ɵã�tan��CDM=tan��CAP=$\frac{3}{6}$=$\frac{1}{2}$��
�ڵ�A1N=MNʱ��tan��CDM=$\frac{3}{4}$����A1M=MNʱ��tan��CDM=$\frac{7}{24}$��
��� �⣺��1����ͼ�٣���Rt��ABC�У�AC=$\sqrt{1{0}^{2}-{8}^{2}}$=6��
��CD=x����A1D=AD=6-x����A1C=$\frac{1}{2}$BC=4��
��Rt��A1CD����x2+42=��6-x��2��
��ã�x=$\frac{5}{3}$��
��CD=$\frac{5}{3}$��
��2����ͼ�ڣ���Rt��A1CD�У�A1D=AD=6-$\frac{9}{4}$=$\frac{15}{4}$��
��A1C=$\sqrt{��\frac{15}{4}��^{2}-��\frac{9}{4}��^{2}}$=3��
��$\frac{CD}{CA}=\frac{3}{8}=\frac{C{A}_{1}}{CB}$��
�ߡ�C=��C��
���CA1D�ס�CBA��
���CA1D=��B��
��A1D��BA��
�ߡ�EA1C=��EA1D+��DA1C=��A+��B=90�㣬
��EA1��AD��
���ı���ADA1E��ƽ���ı��Σ�
��A1D=AD��
��?ADA1E������
��3������ͼ�ۣ���A1M=A1Nʱ������A1��A1H��BC��
���۵��ã���BAC=��DA1E��
��AC��A1H��
���CDM=��MA1H=$\frac{1}{2}$��BAC��
����CAB��ƽ����AP��CB�ڵ�P����P��PQ��AB�ڵ�Q����CP=PQ��
��CP=y��
��Rt��PQB����y2+42=��8-y��2��
��ã�y=3��
��tan��CDM=tan��CAP=$\frac{3}{6}$=$\frac{1}{2}$��
�ڵ�A1N=MNʱ����ͼ�ܣ�
���A1MN=��A1��
�ߡ�A=��A1����CMD=��A1MN��
���A=��CMD��
��tan��A=$\frac{BC}{AC}=\frac{8}{6}$=$\frac{4}{3}$��
��tan��CMD=$\frac{CD}{CM}$=$\frac{4}{3}$��
��tan��CDM=$\frac{3}{4}$��
��A1M=MNʱ����ͼ�ܣ�
���MA1N=��MNA1=��A��
��A1��A1H��BC��H��
tan��A=tan��MNA1=$\frac{4}{3}$=$\frac{{A}_{1}H}{HN}$��
��A1H=4x��HN=3x��A1M=MN=a��MH=a-3x��
��Rt��MA1H��a2-��a-3x��2=��4x��2��
a=$\frac{5}{6}$x��
��CD��A1H��
���CDM=��MA1H��
tan��CDM=tan��MA1H=$\frac{MH}{AH}$=$\frac{\frac{25}{6}x-3x}{4x}$��
��tan��CDM=$\frac{7}{24}$��
��tan��CDM��ֵ��$\frac{1}{2}$��$\frac{3}{4}$��$\frac{7}{24}$��
���� �������ı��ε��ۺ��⣬���������Ǻ��������ε����ʺ��ж������۵����ʡ����������Ƶ����ʺ��ж���������δ֪����������ù��ɶ����з��̣���⼴�ɣ���3�����Ѷȣ��������ۣ��ֱ���һ��Ϊ�����������Ǻ����е�ʽ��������⣮


 ����ʦ��Сһ����ʦ������ҵϵ�д�
����ʦ��Сһ����ʦ������ҵϵ�д� ���100�ֵ�Ԫ�Ż�������ϵ�д�
���100�ֵ�Ԫ�Ż�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -1 | B�� | 0 | C�� | 1 | D�� | 2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 3-a | B�� | -3-a | C�� | a-3 | D�� | a+3 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
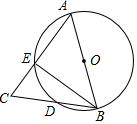 ��ͼ��ABΪ��O��ֱ����AB=AC��BC����O�ڵ�D��AC����O�ڵ�E����BAC=45�㣬���EBC���ڣ�������
��ͼ��ABΪ��O��ֱ����AB=AC��BC����O�ڵ�D��AC����O�ڵ�E����BAC=45�㣬���EBC���ڣ�������| A�� | 22.5�� | B�� | 23�� | C�� | 25�� | D�� | 30�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x��2 | B�� | x��2 | C�� | x��2 | D�� | x��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
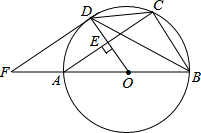 ��ͼ��AB�ǡ�O��ֱ����OD��ֱ��AC�ڵ�E���ҽ���O�ڵ�D������D����O��������BA���ӳ����ཻ�ڵ�F�����н��۲�һ����ȷ���ǣ�������
��ͼ��AB�ǡ�O��ֱ����OD��ֱ��AC�ڵ�E���ҽ���O�ڵ�D������D����O��������BA���ӳ����ཻ�ڵ�F�����н��۲�һ����ȷ���ǣ�������| A�� | ��CDB=��BFD | B�� | ��BAC�ס�OFD | C�� | DF��AC | D�� | OD=BC |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ�ǵ���Ϊ�����εij����壬�����й�����������ͼ��˵����ȷ���ǣ�������
��ͼ�ǵ���Ϊ�����εij����壬�����й�����������ͼ��˵����ȷ���ǣ�������| A�� | ����ͼ������ͼ��ͬ | B�� | ����ͼ������ͼ��ͬ | ||
| C�� | ����ͼ�븩��ͼ��ͬ | D�� | ������ͼ����ͬ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com