
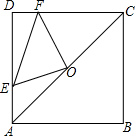
 并且AE=DF.
并且AE=DF.| 5 | 8 |
| 1 |
| 4 |
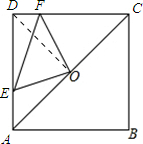 解:(1)在直角三角形ABC中
解:(1)在直角三角形ABC中| AB2+BC2 |
| 2 |
| 1 |
| 4 |
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
| 1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 8 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 5 |
| 8 |


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:初中数学 来源: 题型:
 (2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是
(2013•本溪)如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OB1A1的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是| 1 |
| 310 |
| 1 |
| 310 |
查看答案和解析>>
科目:初中数学 来源:2013年初中毕业升学考试(辽宁本溪卷)数学(解析版) 题型:填空题
如图,点B1是面积为1的等边△OBA的两条中线的交点,以OB1为一边,构造等边△OB1A1(点O,B1,A1按逆时针方向排列),称为第一次构造;点B2是△OBA的两条中线的交点,再以OB2为一边,构造等边△OB2A2(点O,B2,A2按逆时针方向排列),称为第二次构造;以此类推,当第n次构造出的等边△OBnAn的边OAn与等边△OBA的边OB第一次重合时,构造停止.则构造出的最后一个三角形的面积是 .

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 并且AE=DF.
并且AE=DF. .
.查看答案和解析>>
科目:初中数学 来源:2006年福建省泉州市惠安县初中学业质量检查数学试卷(解析版) 题型:解答题
 .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com