
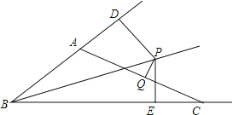
【题目】如图,已知等腰△ABC中,AB=AC,∠BAC=120°,AD⊥BC于点D,点P是BA延长线上一点,点O是线段AD上一点,OP=OC,
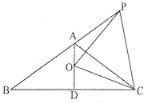
(1)求∠APO+∠DCO的度数;
(2)求证:点P在OC的垂直平分线上.
【答案】(1)30°;(2)详见解析.
【解析】
(1)利用等边对等角,即可证得:∠APO=∠ABO,∠DCO=∠DBO,则∠APO+∠DCO=∠ABO+∠DBO=∠ABD,据此即可求解;
(2)证明∠POC=60°且OP=OC,即可证得△OPC是等边三角形,进而解答即可.
解:(1)如图1,连接OB,
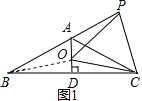
∵AB=AC,AD⊥BC,
∴BD=CD,∠BAD=![]() ∠BAC=
∠BAC=![]() ×120°=60°,
×120°=60°,
∴OB=OC,∠ABC=90°-∠BAD=30°
∵OP=OC,
∴OB=OC=OP,
∴∠APO=∠ABO,∠DCO=∠DBO,
∴∠APO+∠DCO=∠ABO+∠DBO=∠ABD=30°;
(2)∵∠APC+∠DCP+∠PBC=180°,
∴∠APC+∠DCP=150°,
∵∠APO+∠DCO=30°,
∴∠OPC+∠OCP=120°,
∴∠POC=180°-(∠OPC+∠OCP)=60°,
∵OP=OC,
∴△OPC是等边三角形,
∴OP=PC,
∴点P在OC的垂直平分线上


 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:
【题目】已知:如图,点C在∠MON的一边OM上,过点C的直线AB∥ON,CD平分∠ACM,CE⊥CD.
(1)若∠O=50°,求∠BCD的度数;
(2)求证:CE平分∠OCA;
(3)当∠O为多少度时,CA分∠OCD成1:2两部分,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某医药研究所开发一种新药,如果成人按规定的剂量服用,据监测:服药后每毫升血液中含药量y与时间t之间近似满足如图所示曲线:
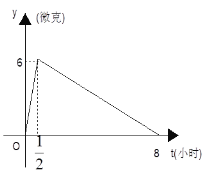
(1)分别求出![]() 和
和![]() 时,y与t之间的函数关系式;
时,y与t之间的函数关系式;
(2)据测定:每毫升血液中含药量不少于4微克时治疗疾病有效,假如某病人一天中第一次服药为7:00,那么服药后几点到几点有效?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点![]() 是边长为
是边长为![]() 的正方形
的正方形![]() 对角线上一个动点(
对角线上一个动点(![]() 与
与![]() 不重合),以
不重合),以![]() 为圆心,
为圆心,![]() 长为半径画圆弧,交线段
长为半径画圆弧,交线段![]() 于点
于点![]() ,联结
,联结![]() ,与
,与![]() 交于点
交于点![]() .设
.设![]() 的长为
的长为![]() ,
,![]() 的面积为
的面积为![]() .
.
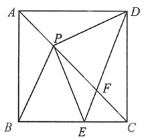
(1)判断![]() 的形状,并说明理由;
的形状,并说明理由;
(2)求![]() 与
与![]() 之间的函数关系式,并写出定义域;
之间的函数关系式,并写出定义域;
(3)当四边形![]() 是梯形时,求出
是梯形时,求出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在“五一”黄金周期间,小明、小亮等同学随家人一同到西安华山游玩,如图是购买门票时,小明与他爸的对话,问题:
(1)小明他们一共去了几个成人?几个学生?
(2)请你帮小明算一算,用哪种方式买票更省钱?并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在△ABC中,∠ABC的平分线BP与AC边的垂直平分线PQ交于点P,过点P分别作PD⊥AB于点D,PE⊥BC于点E,若BE=10cm,AB=6cm,求CE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y1=3x-3的图象与反比例函数y2=![]() 的图象交于点A(a,3),B(-1,b).
的图象交于点A(a,3),B(-1,b).
(1)求a,b的值和反比例函数的表达式.
(2)设点P(h,y1),Q(h,y2)分别是两函数图象上的点.
①试直接写出当y1>y2时h的取值范围;
②若y2- y1=3,试求h的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com